Vector2を使って簡単な直線などを描いてみる

まずは2Dで(x,y)座標の2つのfloat型を保持する構造体Vector2を作成しましょう。

Vector2.hの簡易版を新規作成して以下のコードを実装します。

#ifndef VECTOR2_H_
#define VECTOR2_H_

#include <array> //基本配列と同じ(有限個数)。生配列より便利な機能がある.size()関数とかstd::vector系関数が使える
#include <limits> // std::numeric_limitsで無限大などを使う https://cpprefjp.github.io/reference/limits/numeric_limits.html
#include <cmath> // std::の数学系関数に必要

//【注意】std::vectorとは全く違う。数学で習う【ベクトル】です。ごっちゃにしないで。

//★【UnityのVector演算コード】https://github.com/Unity-Technologies /UnityCsReference/blob/02d565cf3dd0f6b15069ba976064c75dc2705b08/Runtime/Export/Math/Vector2.cs
//★【UnityのMath演算コード】https://github.com/Unity-Technologies /UnityCsReference/blob/master/Runtime/Export/Math/Mathf.cs

// 2変数x,yを持つ構造体。2つの数字をまとめて扱うならXY座標以外にも使えるよ。x,y別々に足したり引いたり面倒でしょう。
struct Vector2
{
   union { // ★共用体unionテクニック https://inemaru.hatenablog.com/entry/2016/03/02/005408
        struct { // [参考ビットサイズ] https://marycore.jp/prog/c-lang/data-type-ranges-and-bit-byte-sizes/
            float x;
            float y;
        }; //[匿名共用体とは] https://code.i-harness.com/ja-jp/q/4d437c
        std::array<float, 2> xy; // float xy[2];と同じ意味 float 2個ぶんのデータサイズでx,y 2個ぶんと一致するので★unionで共用
   }; // unionは異なる複数のものをメモリ上の同一の番地に割り当てられる⇒x,y分けて記述するの面倒なとき配列xy[2]をfor文i=0～2で回せる

   // float型のポインタへ(float*)キャストすればx,yデータの配列の先頭のアドレスを返す
   inline operator float* () const { return (float*)this; }
   // float型のポインタへ(const float*)キャストすればx,yデータの配列の先頭のアドレスを返す
   inline operator const float* () const { return (const float*)this; }

   // 初期化コンストラクタ
   Vector2(float x = 0.0f, float y = 0.0f) //初期化
   {
        this->xy = { x,y }; // たった1行で書ける
        //this->x = x;
        //this->y = y; 2行が上のxyzの様にたった1行で書けるようになる
   }
};

#endif

main.cppを作成して以下のコードでVector2を使って直線や円を描いてみます。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        Vector2 p1{ 100,100 }; // (x,y) = (100,100)の位置の点
        Vector2 p2{ 200,200 }; // (x,y) = (200,200)の位置の点
        Vector2 p3{ 300,300 }; // (x,y) = (300,300)の位置の点
        float r = 30; // 円の半径

        DxLib::DrawLine(p1.x, p1.y, p2.x, p2.y, GetColor(255, 255, 255)); // 線分p1p2を描く

        DxLib::DrawCircle(p3.x, p3.y, r, GetColor(0, 255, 0), FALSE); // 半径rの円(中心:p3)を描く(FALSEで塗りつぶし無し)

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

どうでしょうか？線と円が表示されましたか？

operator +などを定義して、Vector2どうしの足し算などができるようにする

こんどはVector2どうしの足し算などができるように足し算オペレーターoperator +などを定義してみましょう。

Vector2.hに以下のoperator関連のコードを追加します。

#ifndef VECTOR2_H_
#define VECTOR2_H_

#include <array> //基本配列と同じ(有限個数)。生配列より便利な機能がある.size()関数とかstd::vector系関数が使える
#include <limits> // std::numeric_limitsで無限大などを使う https://cpprefjp.github.io/reference/limits/numeric_limits.html
#include <cmath> // std::の数学系関数に必要

//【注意】std::vectorとは全く違う。数学で習う【ベクトル】です。ごっちゃにしないで。

//★【UnityのVector演算コード】https://github.com/Unity-Technologies /UnityCsReference/blob/02d565cf3dd0f6b15069ba976064c75dc2705b08/Runtime/Export/Math/Vector2.cs
//★【UnityのMath演算コード】https://github.com/Unity-Technologies /UnityCsReference/blob/master/Runtime/Export/Math/Mathf.cs

// 2変数x,yを持つ構造体。2つの数字をまとめて扱うならXY座標以外にも使えるよ。x,y別々に足したり引いたり面倒でしょう。
struct Vector2
{
   union { // ★共用体unionテクニック https://inemaru.hatenablog.com/entry/2016/03/02/005408
        struct { // [参考ビットサイズ] https://marycore.jp/prog/c-lang/data-type-ranges-and-bit-byte-sizes/
            float x;
            float y;
        }; //[匿名共用体とは] https://code.i-harness.com/ja-jp/q/4d437c
        std::array<float, 2> xy; // float xy[2];と同じ意味 float 2個ぶんのデータサイズでx,y 2個ぶんと一致するので★unionで共用
   }; // unionは異なる複数のものをメモリ上の同一の番地に割り当てられる⇒x,y分けて記述するの面倒なとき配列xy[2]をfor文i=0～2で回せる

   // float型のポインタへ(float*)キャストすればx,yデータの配列の先頭のアドレスを返す
   inline operator float* () const { return (float*)this; }
   // float型のポインタへ(const float*)キャストすればx,yデータの配列の先頭のアドレスを返す
   inline operator const float* () const { return (const float*)this; }

   // 初期化コンストラクタ
   Vector2(float x = 0.0f, float y = 0.0f) //初期化
   {
        this->xy = { x,y }; // たった1行で書ける
        //this->x = x;
        //this->y = y; 2行が上のxyzの様にたった1行で書けるようになる
   }

    /*-----　演算子オーバーロード　-----*/

    // 逆ベクトル
    inline Vector2 operator -() const
    {
        return Vector2{ -this->x, -this->y };
    }

    // Vectorをそのまま足し合わせる
    inline Vector2 operator + () const
    {
        return *this;
    }

    Vector2& operator += (const Vector2 add_v2)
    {
        this->x += add_v2.x;
        this->y += add_v2.y;

        return *this; //*thisを返すことで v1 + v2 + v3見たく数珠繋ぎできる
    }

    Vector2& operator -= (const Vector2 minus_v2)
    {
        this->x -= minus_v2.x;
        this->y -= minus_v2.y;

        return *this;
    }

    Vector2& operator *= (float multiply_num)
    {
        this->x *= multiply_num;
        this->y *= multiply_num;

        return *this;
    }

    // 0.fで割ったときは±無限大を返す
    inline Vector2& operator /= (float divide_num)
    {
        if (divide_num == 0.0f) // 0で割ったら±無限大を返す
        {
            *this = Vector2{ ((this->x < 0) ? 1 : -1) * std::numeric_limits<float>::infinity(),
                            ((this->y < 0) ? 1 : -1) * std::numeric_limits<float>::infinity() };
            return *this;
        }

        this->x /= divide_num;
        this->y /= divide_num;

        return *this;
    }

    // 代入演算子 x,y,zを全部 change_numに変える
    Vector2& operator = (float change_num)
    {
        this->x = change_num;
        this->y = change_num;

        return *this;
    }

    // 一致演算子 x,y,zを全部一致するか一つでも違えばfalse
    bool operator == (const Vector2& v2_other)
    {
        if (this->x != v2_other.x) return false;
        if (this->y != v2_other.y) return false;
        return true;
    }

    // 不一致演算子一致演算子の逆
    bool operator != (const Vector2& v2_other)
    {
        return !(*this == v2_other);
    }

};

// Vector2どうしの足し算割り算掛け算割り算などの基本演算のグローバル定義

// Vector同士の足し算 x,y個別に足し合わせる
inline Vector2 operator + (const Vector2& left, const Vector2& right)
{
    Vector2 v2; //注意 vec1 = vec1 + vec2のとき vec1の数値が書き変わったら嫌だからv3を新たに用意
    v2.x = left.x + right.x; //[コレはダメ] left.x = left.x + right.x;
    v2.y = left.y + right.y;

    return v2;
}

// Vector同士の引き算 x,y個別に足し合わせる
inline Vector2 operator - (const Vector2& left, const Vector2& right)
{
    Vector2 v2; //注意 vec1 = vec1 - vec2のとき vec1の数値が書き変わったら嫌だからv2を新たに用意
    v2.x = left.x - right.x; //[コレはダメ] left.x = left.x - right.x;
    v2.y = left.y - right.y;

    return v2;
}

// Vectorと数値の掛け算 x,y個別に掛け合わせる
inline Vector2 operator * (const Vector2& left, float right)
{
    Vector2 v2;
    v2.x = left.x * right;
    v2.y = left.y * right;

    return v2;
}

// 数値とVectorの掛け算 x,y個別に掛け合わせる
inline Vector2 operator * (float left, const Vector2& right)
{
    Vector2 v2;
    v2.x = left * right.x;
    v2.y = left * right.y;

    return v2;
}

// Vectorと数値の割り算 x,y,z個別に割り合わせる
// 0.fで割ると±無限大を返す
inline Vector2 operator / (const Vector2& left, float right)
{
    if (right == 0.0f) // 0で割ったら±無限大を返す
        return Vector2{ ((left.x < 0) ? 1 : -1) * std::numeric_limits<float>::infinity(),
                        ((left.y < 0) ? 1 : -1) * std::numeric_limits<float>::infinity() };

    Vector2 v2;
    v2.x = left.x / right;
    v2.y = left.y / right;

    return v2;
}

// 比較不等号 < 演算子
inline bool operator < (const Vector2& left, const Vector2& right)
{
    if (left.x != right.x) return left.x < right.x;
    return left.y < right.y;
}

// 比較不等号 > 演算子
inline bool operator > (const Vector2& left, const Vector2& right)
{
    if (left.x != right.x) return left.x > right.x;
    return left.y > right.y;
}

// 比較不等号 <= 演算子
inline bool operator <= (const Vector2& left, const Vector2& right)
{
    return    !(left > right);
}

// 比較不等号 >= 演算子
inline bool operator >= (const Vector2& left, const Vector2& right)
{
    return    !(left < right);
}

#endif

main.cppを変更してVector2どうしの足し算や引き算を使って線を描いてみます。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        Vector2 p1{ 100,100 }; // (x,y) = (100,100)の位置の点
        Vector2 p2{ 200,200 }; // (x,y) = (200,200)の位置の点
        Vector2 p3{ 300,300 }; // (x,y) = (300,300)の位置の点
        float r = 30; // 円の半径

        Vector2 v13 = p3 - p1; // 終点p3 から始点p1を引くとp1からp3へ向かう方向ベクトルになる

        DxLib::DrawLine(p1.x, p1.y, p1.x + v13.x * 2, p1.y + v13.y * 2, GetColor(255, 0, 255)); // 線分p1p3の2倍した線を描く

        DxLib::DrawLine(p1.x, p1.y, p1.x + v13.x, p1.y + v13.y, GetColor(255, 255, 255)); // 線分p1p3を描く

        DxLib::DrawCircle(p3.x, p3.y, r, GetColor(0, 255, 0), FALSE); // 半径rの円(中心:p3)を描く(FALSEで塗りつぶし無し)

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょうか？ベクトルを足したり、引いたり、掛け算したりするとどうなるか理解できましたか？
ベクトルの終点 - 始点の計算をすると始点→終点に向かう方向ベクトルとなり、
ベクトルの始点 + 方向ベクトルすると終点に到着することが理解できたらOKです。
また、方向ベクトル×2 すると線の長さが2倍になっていることも直感的に理解できるとよいです。

Unityの定義に習って、zeroベクトルupベクトルなどの定義を追加する

UnityのVector2の定義は以下のサイトでコードが見れたりしますので参考にしてzeroやupなどをC#ではなくC++として定義してましょう。

数学グラフクラスを作成して数学っぽいマス目を引いたり、画面上y方向プラス、画面中心(0,0)、(x,y)が(3,9)のとき(30,90)など拡大した位置に描く

MathGraph2D.hを新規作成して数学っぽいマス目グリッドを描いたり、画面上方向がy方向プラスにしたり、
(x,y)が(3,9)のときに(30,90)など拡大した位置に描いて見やすくできるようにグラフのスケールを設定できるようにするクラスのコードを追加します。

#ifndef MATHGRAPH_H_
#define MATHGRAPH_H_

#include "DxLib.h"
#include "Vector2.h"
#include "Screen.h"
#include <cmath>
#include <string>

// 数学のグラフを描く(DXで普通に描くと左上 0,0 で↓方向が+なので数学らしくないので)
class MathGraph2D
{
public:
   Vector2 pos; // グラフを描く起点(100,100なら左上から→に100,↓に100の位置がグラフの原点)
   //Vector2 origin; // グラフ原点
   float scale; // グラフのスケール(1/10 なら10ドットで1目盛りぶん)
   Vector2 grid; // (10,10)なら10おきにグリッドを描く
   MathGraph2D(Vector2 position, float scale = 5.0f, Vector2 grid = { 5.0f,5.0f })
        : pos{ Vector2((int)position.x,(int)position.y)}, scale{scale}, grid{ Vector2((int)grid.x,(int)grid.y) }
   {}

   virtual ~MathGraph2D(){};

   inline Vector2 graphPos(Vector2 mousePos) { return Vector2{ (mousePos.x - pos.x) / scale, (-mousePos.y + pos.y) / scale }; }
   inline Vector2 graphPosInt(Vector2 mousePos) { return Vector2{ (float)((int)((mousePos.x - pos.x) / scale)), (float)((int)((-mousePos.y + pos.y) / scale)) }; }

   int DrawString(float x, float y, const TCHAR* String, unsigned int Color, unsigned int EdgeColor DEFAULTPARAM(= 0))
   {   // y方向にはマイナス - をつけて上方向↑がプラスになるようにして描く
        return DxLib::DrawString(pos.x + x * scale, pos.y - y * scale, String, Color, EdgeColor);
   }

   int DrawLine(float x1, float y1, float x2, float y2, unsigned int Color, int Thickness DEFAULTPARAM(= 1))
   {   // y方向にはマイナス - をつけて上方向↑がプラスになるようにして描く
        return DxLib::DrawLine(pos.x + x1 * scale, pos.y - y1 * scale, pos.x + x2 * scale, pos.y - y2 * scale, Color, Thickness);
   }

    int DrawTriangle(float x1, float y1, float x2, float y2, float x3, float y3, unsigned int Color, int FillFlag DEFAULTPARAM(= TRUE))
    {    // y方向にはマイナス - をつけて上方向↑がプラスになるようにして描く
        return DxLib::DrawTriangle(pos.x + x1 * scale, pos.y - y1 * scale,
                                   pos.x + x2 * scale, pos.y - y2 * scale,
                                   pos.x + x3 * scale, pos.y - y3 * scale, Color, FillFlag);
    }

   // 矢印→を線のかわりに描く
   int DrawArrow(float x1, float y1, float w1, float h1, float x2, float y2, float w2, float h2, unsigned int Color, int Thickness DEFAULTPARAM(= 1))
   {   // y方向にはマイナス - をつけて上方向↑がプラスになるようにして描く
        //[矢印の描きかた] https://ameblo.jp/tomi-omiya/entry-12641374677.html
        if (w1 != 0.0f && h1 != 0.0f)
        {
            float theta1 = -std::atan2(y1 - y2, x1 - x2), cos1 = std::cosf(theta1), sin1 = std::sinf(theta1);
            float angle = theta1 / DX_PI * 180;
            DrawTriangle(x1, y1, x1 - h1 * cos1 - w1 / 2 * sin1, y1 + h1 * sin1 - w1 / 2 * cos1,
                                 x1 - h1 * cos1 + w1 / 2 * sin1, y1 + h1 * sin1 + w1 / 2 * cos1, Color, TRUE);
        }
        if (w2 != 0.0f && h2 != 0.0f)
        {
            float theta2 = -std::atan2(y2 - y1, x2 - x1), cos2 = std::cosf(theta2), sin2 = std::sinf(theta2);
            DrawTriangle(x2, y2, x2 - h2 * cos2 - w2 / 2 * sin2, y2 + h2 * sin2 - w2 / 2 * cos2,
                                x2 - h2 * cos2 + w2 / 2 * sin2, y2 + h2 * sin2 + w2 / 2 * cos2, Color, TRUE);
        }
        return DxLib::DrawLine(pos.x + x1 * scale, pos.y - y1 * scale, pos.x + x2 * scale, pos.y - y2 * scale, Color, Thickness);
   }

   int DrawLineBox(float x1, float y1, float x2, float y2, unsigned int Color)
   {   // y方向にはマイナス - をつけて上方向↑がプラスになるようにして描く
        return DxLib::DrawLineBox(pos.x + x1 * scale, pos.y - y1 * scale, pos.x + x2 * scale, pos.y - y2 * scale, Color);
   }

   int DrawFillBox(float x1, float y1, float x2, float y2, unsigned int Color)
   {   // y方向にはマイナス - をつけて上方向↑がプラスになるようにして描く
        return DxLib::DrawFillBox(pos.x + x1 * scale, pos.y - y1 * scale, pos.x + x2 * scale, pos.y - y2 * scale, Color);
   }

   int   DrawCircle(float x, float y, int r, unsigned int Color, int FillFlag DEFAULTPARAM(= TRUE), int LineThickness DEFAULTPARAM(= 1))
   {   // y方向にはマイナス - をつけて上方向↑がプラスになるようにして描く
        return DxLib::DrawCircle(pos.x + x * scale, pos.y - y * scale, r * scale, Color, FillFlag, LineThickness);
   }

   int   DrawPoint(float x, float y, int r, unsigned int Color, int FillFlag DEFAULTPARAM(= TRUE), int LineThickness DEFAULTPARAM(= 1))
   {   // y方向にはマイナス - をつけて上方向↑がプラスになるようにして描く
        return DxLib::DrawCircle(pos.x + x * scale, pos.y - y * scale, r, Color, FillFlag, LineThickness);
   }

   // グラフの目盛りの縦横グリッドを描く
   void DrawGrid(unsigned int Color, int Thickness DEFAULTPARAM(= 1))
   {
        float test = std::fmodf(pos.x, grid.x * scale);

        for (int x = std::fmodf(pos.x, grid.x * scale); x < Screen::Width; x += grid.x * scale)
            DxLib::DrawLine(x, 0, x, Screen::Height,
                            (x == (int)pos.x) ? GetColor(255,0,0) : // グラフの原点を通る線は色を変える
                            ((x-(int)pos.x) % (int)(grid.x * scale * 10) == 0) ? GetColor(255, 255, 255) : Color, // 10マスおきに色を変える
                            Thickness);

        for (int y = std::fmodf(pos.y, grid.y * scale); y <= Screen::Height; y += grid.y * scale)
            DxLib::DrawLine(0, y, Screen::Width, y,
                (y == (int)pos.y) ? GetColor(0, 0, 255) : // グラフの原点を通る線は色を変える
                ((y - (int)pos.y) % (int)(grid.y * scale * 10) == 0) ? GetColor(255, 255, 255) : Color, // 10マスおきに色を変える
                Thickness);
   }
};

#endif

main.cppを変更して数学グラフクラスMathGraph2Dを通して円や線を描いてみます。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p1{ 1,1 }; // (x,y) = (1,1)の位置の点
        Vector2 p2{ 2,2 }; // (x,y) = (2,2)の位置の点
        Vector2 p3{ 3,3 }; // (x,y) = (3,3)の位置の点
        float r = 1; // 円の半径

        Vector2 v13 = p3 - p1; // 終点p3 から始点p1を引くとp1からp3へ向かう方向ベクトルになる

        mathGraph.DrawLine(p1.x, p1.y, p1.x + Vector2::up.x * 3, p1.y + Vector2::up.y * 3, GetColor(0, 255, 255)); // upベクトルを3倍した線を描く

        mathGraph.DrawLine(p1.x, p1.y, p1.x + v13.x * 2, p1.y + v13.y * 2, GetColor(255, 0, 255)); // 線分p1p3の2倍した線を描く

        mathGraph.DrawLine(p1.x, p1.y, p1.x + v13.x, p1.y + v13.y, GetColor(255, 255, 255)); // 線分p1p3を描く

        mathGraph.DrawCircle(p3.x, p3.y, r, GetColor(0, 255, 0), FALSE); // 半径rの円(中心:p3)を描く(FALSEで塗りつぶし無し)

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょうか？これで水色のup上方向ベクトルも上向きになり、ベクトルの数字も(1,1)など手で計算しやすいスケール感に収めることができ、算数しやすくなったと思います。

数学クラスMyMathを作成して円と円の当たり判定をしてみる

MyMath.hを新規作成してπなどの定義や円と円の当たり判定の関数を定義します。

#ifndef MYMATH_H_
#define MYMATH_H_

#include "Vector2.h" // 線との当たり判定にVector2を使う

#include <cmath>

// 数学関連クラス
class MyMath
{
public:
   static const float Sqrt2; // = 1.41421356237f;　// √2

   static const float PI; // = 3.14159265359f; // 円周率
   static const float Deg2Rad; // = PI / 180f; // 度からラジアンに変換する定数

    /// <summary>
    /// 円と円が重なっているかを調べる
    /// </summary>
    /// <param name="pc1">円1の中心pc1</param>
    /// <param name="radius1">円1の半径</param>
    /// <param name="pc2">円2の中心pc2</param>
    /// <param name="radius2">円2の半径</param>
    /// <returns>重なっていればtrue、重なっていなければfalseを返却する</returns>
    static bool CircleCircleIntersection(
        Vector2 pc1, float radius1,
        Vector2 pc2, float radius2)
    {
        return ((pc1.x - pc2.x) * (pc1.x - pc2.x) + (pc1.y - pc2.y) * (pc1.y - pc2.y))
            < ((radius1 + radius2) * (radius1 + radius2));
    }

};

#endif

MyMath.cppを新規作成してπなどのstatic定義の初期値を設定します。

#include "MyMath.h"

const float MyMath::Sqrt2 = 1.41421356237f;//(floatは有効桁は実質7桁まで正確だがそれ以降は環境によって誤差出るよ)

const float MyMath::PI = 3.14159265359f; // 円周率
const float MyMath::Deg2Rad = PI / 180; // 度からラジアンに変換する定数

main.cppを変更して円と円の当たり判定を試してみます。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p1{ 1,1 }; // (x,y) = (1,1)の位置の点
        Vector2 p2{ 2,2 }; // (x,y) = (2,2)の位置の点
        Vector2 p3{ 3,3 }; // (x,y) = (3,3)の位置の点
        float r = 1; // 円の半径

        Vector2 pc1{ 6,5 }; // 円1の中心
        float r1 = 2; // 円1の半径
        Vector2 pc2{ 10,9 }; // 円2の中心
        float r2 = 3; // 円1の半径

        Vector2 v13 = p3 - p1; // 終点p3 から始点p1を引くとp1からp3へ向かう方向ベクトルになる

        // 円1と円2が当たっているかの判定
        bool isCollision12 = MyMath::CircleCircleIntersection(pc1, r1, pc2, r2);

        mathGraph.DrawCircle(pc1.x, pc1.y, r1, (isCollision12) ? GetColor(255, 0, 0): GetColor(255, 255, 255), FALSE); // 円1を描く
        mathGraph.DrawCircle(pc2.x, pc2.y, r2, (isCollision12) ? GetColor(255, 0, 0) : GetColor(255, 255, 255), FALSE); // 円2を描く

        mathGraph.DrawLine(p1.x, p1.y, p1.x + Vector2::up.x * 3, p1.y + Vector2::up.y * 3, GetColor(0, 255, 255)); // upベクトルを3倍した線を描く

        mathGraph.DrawLine(p1.x, p1.y, p1.x + v13.x * 2, p1.y + v13.y * 2, GetColor(255, 0, 255)); // 線分p1p3の2倍した線を描く

        mathGraph.DrawLine(p1.x, p1.y, p1.x + v13.x, p1.y + v13.y, GetColor(255, 255, 255)); // 線分p1p3を描く

        mathGraph.DrawCircle(p3.x, p3.y, r, GetColor(0, 255, 0), FALSE); // 半径rの円(中心:p3)を描く(FALSEで塗りつぶし無し)

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

さて、円1と円2は触れていないので白色GetColor(255,255,255)で描かれているはずです。
こんどは円2の中心を{10,9}ではなく{8,9}に変えてみましょう。

main.cppを変更して円2の中心を{10,9}ではなく{8,9}に変えます。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p1{ 1,1 }; // (x,y) = (1,1)の位置の点
        Vector2 p2{ 2,2 }; // (x,y) = (2,2)の位置の点
        Vector2 p3{ 3,3 }; // (x,y) = (3,3)の位置の点
        float r = 1; // 円の半径

        Vector2 pc1{ 6,5 }; // 円1の中心
        float r1 = 2; // 円1の半径
        Vector2 pc2{ 8,9 }; // 円2の中心
        float r2 = 3; // 円1の半径

        Vector2 v13 = p3 - p1; // 終点p3 から始点p1を引くとp1からp3へ向かう方向ベクトルになる

        // 円1と円2が当たっているかの判定
        bool isCollision12 = MyMath::CircleCircleIntersection(pc1, r1, pc2, r2);

        mathGraph.DrawCircle(pc1.x, pc1.y, r1, (isCollision12) ? GetColor(255, 0, 0): GetColor(255, 255, 255), FALSE); // 円1を描く
        mathGraph.DrawCircle(pc2.x, pc2.y, r2, (isCollision12) ? GetColor(255, 0, 0) : GetColor(255, 255, 255), FALSE); // 円2を描く

        mathGraph.DrawLine(p1.x, p1.y, p1.x + Vector2::up.x * 3, p1.y + Vector2::up.y * 3, GetColor(0, 255, 255)); // upベクトルを3倍した線を描く

        mathGraph.DrawLine(p1.x, p1.y, p1.x + v13.x * 2, p1.y + v13.y * 2, GetColor(255, 0, 255)); // 線分p1p3の2倍した線を描く

        mathGraph.DrawLine(p1.x, p1.y, p1.x + v13.x, p1.y + v13.y, GetColor(255, 255, 255)); // 線分p1p3を描く

        mathGraph.DrawCircle(p3.x, p3.y, r, GetColor(0, 255, 0), FALSE); // 半径rの円(中心:p3)を描く(FALSEで塗りつぶし無し)

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

さて、こんどは円1と円2は触れいるので赤色GetColor(255,0,0)で描かれているはずです。
円と円の当たり判定をMyMathクラスで正しくできたことが確認できました。

Vector2にベクトルの大きさを三平方の定理で計算するmagnitude関数を追加する

Vector2.hに関数を追加で定義します。

#ifndef VECTOR2_H_
#define VECTOR2_H_

#include <array> //基本配列と同じ(有限個数)。生配列より便利な機能がある.size()関数とかstd::vector系関数が使える
#include <limits> // std::numeric_limitsで無限大などを使う https://cpprefjp.github.io/reference/limits/numeric_limits.html
#include <cmath> // std::の数学系関数に必要

//【注意】std::vectorとは全く違う。数学で習う【ベクトル】です。ごっちゃにしないで。

//★【UnityのVector演算コード】https://github.com/Unity-Technologies /UnityCsReference/blob/02d565cf3dd0f6b15069ba976064c75dc2705b08/Runtime/Export/Math/Vector3.cs
//★【UnityのMath演算コード】https://github.com/Unity-Technologies /UnityCsReference /blob/master/Runtime/Export/Math/Mathf.cs

// 2変数x,yを持つ構造体。2つの数字をまとめて扱うならXY座標以外にも使えるよ。x,y別々に足したり引いたり面倒でしょう。
struct Vector2
{
   union { // ★共用体unionテクニック https://inemaru.hatenablog.com/entry/2016/03/02/005408
        struct { // [参考ビットサイズ] https://marycore.jp/prog/c-lang/data-type-ranges-and-bit-byte-sizes/
            float x;
            float y;
        }; //[匿名共用体とは] https://code.i-harness.com/ja-jp/q/4d437c
        std::array<float, 2> xy; // float xy[2];と同じ意味 float 2個ぶんのデータサイズでx,y 2個ぶんと一致するので★unionで共用
   }; // unionは異なる複数のものをメモリ上の同一の番地に割り当てられる⇒x,y分けて記述するの面倒なとき配列xy[2]をfor文i=0～2で回せる

   // float型のポインタへ(float*)キャストすればx,yデータの配列の先頭のアドレスを返す
   inline operator float* () const { return (float*)this; }
   // float型のポインタへ(const float*)キャストすればx,yデータの配列の先頭のアドレスを返す
   inline operator const float* () const { return (const float*)this; }

   // 初期化コンストラクタ
   Vector2(float x = 0.0f, float y = 0.0f) //初期化
   {
        this->xy = { x,y }; // たった1行で書ける
        //this->x = x;
        //this->y = y; 2行が上のxyzの様にたった1行で書けるようになる
   }

    // Unityのstatic変数を参考に https://docs.unity3d.com/ja/current/ScriptReference/Vector3.html
    static const Vector2 zero;// = { 0.f, 0.f };
    static const Vector2 one; // = { 1.f, 1.f };
    static const Vector2 up; // = { 0.f, 1.f };
    static const Vector2 down;// = { 0.f, -1.f };
    static const Vector2 left; // = { -1.f, 0.f };
    static const Vector2 right;// = { 1.f, 0.f };
    //[負の値の最小値] https://stackoverflow.com/questions/20016600/negative-infinity
    static const Vector2 negativeInfinity;// = { -std::numeric_limits<float>::infinity(), .. };
    //[極大値]https://cpprefjp.github.io/reference/limits/numeric_limits/lowest.html
    static const Vector2 positiveInfinity;// = { std::numeric_limits<float>::infinity(), .. };

    // ベクトルの長さ(0から点(x,y,z)までの距離)
    inline float magnitude() const //[後ろにconstをつけないと..] https://www7b.biglobe.ne.jp/~robe/cpphtml/html02/cpp02010.html
    {
        return std::sqrt(x * x + y * y); // √(x*x + y*y)
    };

    // ベクトルの 2 乗の長さを返します(平方根しないぶん計算速い)
    inline float sqrMagnitude() const //[後ろにconstをつけないと..] https://www7b.biglobe.ne.jp/~robe/cpphtml/html02/cpp02010.html
    {
        return x * x + y * y; // x*x + y*y
    };

    /*-----　演算子オーバーロード　-----*/

    // 逆ベクトル
    inline Vector2 operator -() const
    {
        return Vector2{ -this->x, -this->y };
    }

    // Vectorをそのまま足し合わせる
    inline Vector2 operator + () const
    {
        return *this;
    }

    Vector2& operator += (const Vector2 add_v2)
    {
        this->x += add_v2.x;
        this->y += add_v2.y;

        return *this; //*thisを返すことで v1 + v2 + v3見たく数珠繋ぎできる
    }

    Vector2& operator -= (const Vector2 minus_v2)
    {
        this->x -= minus_v2.x;
        this->y -= minus_v2.y;

        return *this;
    }

    Vector2& operator *= (float multiply_num)
    {
        this->x *= multiply_num;
        this->y *= multiply_num;

        return *this;
    }

    // 0.fで割ったときは±無限大を返す
    inline Vector2& operator /= (float divide_num)
    {
        if (divide_num == 0.0f) // 0で割ったら±無限大を返す
        {
            *this = Vector2{ ((this->x < 0) ? 1 : -1) * std::numeric_limits<float>::infinity(),
                            ((this->y < 0) ? 1 : -1) * std::numeric_limits<float>::infinity() };
            return *this;
        }

        this->x /= divide_num;
        this->y /= divide_num;

        return *this;
    }

    // 代入演算子 x,y,zを全部 change_numに変える
    Vector2& operator = (float change_num)
    {
        this->x = change_num;
        this->y = change_num;

        return *this;
    }

    // 一致演算子 x,y,zを全部一致するか一つでも違えばfalse
    bool operator == (const Vector2& v2_other)
    {
        if (this->x != v2_other.x) return false;
        if (this->y != v2_other.y) return false;
        return true;
    }

    // 不一致演算子一致演算子の逆
    bool operator != (const Vector2& v2_other)
    {
        return !(*this == v2_other);
    }

};

// Vector2どうしの足し算割り算掛け算割り算などの基本演算のグローバル定義

// Vector同士の足し算 x,y個別に足し合わせる
inline Vector2 operator + (const Vector2& left, const Vector2& right)
{
    Vector2 v2; //注意 vec1 = vec1 + vec2のとき vec1の数値が書き変わったら嫌だからv3を新たに用意
    v2.x = left.x + right.x; //[コレはダメ] left.x = left.x + right.x;
    v2.y = left.y + right.y;

    return v2;
}

// Vector同士の引き算 x,y個別に足し合わせる
inline Vector2 operator - (const Vector2& left, const Vector2& right)
{
    Vector2 v2; //注意 vec1 = vec1 - vec2のとき vec1の数値が書き変わったら嫌だからv2を新たに用意
    v2.x = left.x - right.x; //[コレはダメ] left.x = left.x - right.x;
    v2.y = left.y - right.y;

    return v2;
}

// Vectorと数値の掛け算 x,y個別に掛け合わせる
inline Vector2 operator * (const Vector2& left, float right)
{
    Vector2 v2;
    v2.x = left.x * right;
    v2.y = left.y * right;

    return v2;
}

// 数値とVectorの掛け算 x,y個別に掛け合わせる
inline Vector2 operator * (float left, const Vector2& right)
{
    Vector2 v2;
    v2.x = left * right.x;
    v2.y = left * right.y;

    return v2;
}

// Vectorと数値の割り算 x,y,z個別に割り合わせる
// 0.fで割ると±無限大を返す
inline Vector2 operator / (const Vector2& left, float right)
{
    if (right == 0.0f) // 0で割ったら±無限大を返す
        return Vector2{ ((left.x < 0) ? 1 : -1) * std::numeric_limits<float>::infinity(),
                        ((left.y < 0) ? 1 : -1) * std::numeric_limits<float>::infinity() };

    Vector2 v2;
    v2.x = left.x / right;
    v2.y = left.y / right;

    return v2;
}

// 比較不等号 < 演算子
inline bool operator < (const Vector2& left, const Vector2& right)
{
    if (left.x != right.x) return left.x < right.x;
    return left.y < right.y;
}

// 比較不等号 > 演算子
inline bool operator > (const Vector2& left, const Vector2& right)
{
    if (left.x != right.x) return left.x > right.x;
    return left.y > right.y;
}

// 比較不等号 <= 演算子
inline bool operator <= (const Vector2& left, const Vector2& right)
{
    return    !(left > right);
}

// 比較不等号 >= 演算子
inline bool operator >= (const Vector2& left, const Vector2& right)
{
    return    !(left < right);
}

// ベクトルの 2 乗の長さを返します(平方根しないぶん計算速い)
inline float sqrMagnitude(const Vector2& vec)
{
    return vec.x * vec.x + vec.y * vec.y; // x*x + y*y
}

// ベクトルの長さ(原点0から点(x,y)までの距離)
inline float magnitude(const Vector2& vec)
{
    return std::sqrt(sqrMagnitude(vec)); // √x*x + y*y
}

#endif

MyMath.hを変更して円と円の距離をsqrMagnitude関数(円どうしの距離の2乗)を使った形に置き換えてみましょう。

#ifndef MYMATH_H_
#define MYMATH_H_

#include "Vector2.h" // 線との当たり判定にVector2を使う

#include <cmath>

// 数学関連クラス
class MyMath
{
public:
   static const float Sqrt2; // = 1.41421356237f;　// √2

   static const float PI; // = 3.14159265359f; // 円周率
   static const float Deg2Rad; // = PI / 180f; // 度からラジアンに変換する定数

    /// <summary>
    /// 円と円が重なっているかを調べる
    /// </summary>
    /// <param name="pc1">円1の中心pc1</param>
    /// <param name="radius1">円1の半径</param>
    /// <param name="pc2">円2の中心pc2</param>
    /// <param name="radius2">円2の半径</param>
    /// <returns>重なっていればtrue、重なっていなければfalseを返却する</returns>
    static bool CircleCircleIntersection(
        Vector2 pc1, float radius1,
        Vector2 pc2, float radius2)
    {
        return (pc1 - pc2).sqrMagnitude() < ((radius1 + radius2) * (radius1 + radius2));
    }

};

#endif

さて、だいぶ式がすっきりしましたが、これでもちゃんと円どうしの当たり判定を計算できます。
magnitude系関数はつまり「三平方の定理」の距離を求める処理を関数という機能に置き換えた便利ツールと考えるとイメージしやすいかもしれません。

Vector2に内積dotと外積cross関数を追加してMyMathクラスで円と線の当たり判定をできるようにする

Vector2.hに関数を追加で定義します。

#ifndef VECTOR2_H_
#define VECTOR2_H_

#include <array> //基本配列と同じ(有限個数)。生配列より便利な機能がある.size()関数とかstd::vector系関数が使える
#include <limits> // std::numeric_limitsで無限大などを使う https://cpprefjp.github.io/reference/limits/numeric_limits.html
#include <cmath> // std::の数学系関数に必要

//【注意】std::vectorとは全く違う。数学で習う【ベクトル】です。ごっちゃにしないで。

//★【UnityのVector演算コード】https://github.com/Unity-Technologies /UnityCsReference/blob/02d565cf3dd0f6b15069ba976064c75dc2705b08/Runtime/Export/Math/Vector3.cs
//★【UnityのMath演算コード】https://github.com/Unity-Technologies /UnityCsReference /blob/master/Runtime/Export/Math/Mathf.cs

// 2変数x,yを持つ構造体。2つの数字をまとめて扱うならXY座標以外にも使えるよ。x,y別々に足したり引いたり面倒でしょう。
struct Vector2
{
   union { // ★共用体unionテクニック https://inemaru.hatenablog.com/entry/2016/03/02/005408
        struct { // [参考ビットサイズ] https://marycore.jp/prog/c-lang/data-type-ranges-and-bit-byte-sizes/
            float x;
            float y;
        }; //[匿名共用体とは] https://code.i-harness.com/ja-jp/q/4d437c
        std::array<float, 2> xy; // float xy[2];と同じ意味 float 2個ぶんのデータサイズでx,y 2個ぶんと一致するので★unionで共用
   }; // unionは異なる複数のものをメモリ上の同一の番地に割り当てられる⇒x,y分けて記述するの面倒なとき配列xy[2]をfor文i=0～2で回せる

   // float型のポインタへ(float*)キャストすればx,yデータの配列の先頭のアドレスを返す
   inline operator float* () const { return (float*)this; }
   // float型のポインタへ(const float*)キャストすればx,yデータの配列の先頭のアドレスを返す
   inline operator const float* () const { return (const float*)this; }

   // 初期化コンストラクタ
   Vector2(float x = 0.0f, float y = 0.0f) //初期化
   {
        this->xy = { x,y }; // たった1行で書ける
        //this->x = x;
        //this->y = y; 2行が上のxyzの様にたった1行で書けるようになる
   }

    // Unityのstatic変数を参考に https://docs.unity3d.com/ja/current/ScriptReference/Vector3.html
    static const Vector2 zero;// = { 0.f, 0.f };
    static const Vector2 one; // = { 1.f, 1.f };
    static const Vector2 up; // = { 0.f, 1.f };
    static const Vector2 down;// = { 0.f, -1.f };
    static const Vector2 left; // = { -1.f, 0.f };
    static const Vector2 right;// = { 1.f, 0.f };
    //[負の値の最小値] https://stackoverflow.com/questions/20016600/negative-infinity
    static const Vector2 negativeInfinity;// = { -std::numeric_limits<float>::infinity(), .. };
    //[極大値]https://cpprefjp.github.io/reference/limits/numeric_limits/lowest.html
    static const Vector2 positiveInfinity;// = { std::numeric_limits<float>::infinity(), .. };

    // ベクトルの長さ(0から点(x,y,z)までの距離)
    inline float magnitude() const //[後ろにconstをつけないと..] https://www7b.biglobe.ne.jp/~robe/cpphtml/html02/cpp02010.html
    {
        return std::sqrt(x * x + y * y); // √(x*x + y*y)
    };

    // ベクトルの 2 乗の長さを返します(平方根しないぶん計算速い)
    inline float sqrMagnitude() const //[後ろにconstをつけないと..] https://www7b.biglobe.ne.jp/~robe/cpphtml/html02/cpp02010.html
    {
        return x * x + y * y; // x*x + y*y
    };

    // 正規化したベクトルを返す
    Vector2 normalized() const //[後ろにconstをつけないと..] https://www7b.biglobe.ne.jp/~robe/cpphtml/html02/cpp02010.html
    {
        float mag = magnitude();
        if (mag < 0.00001f) // ほぼ0ベクトルか？
            return *this;
        else
            return Vector2{ x / mag, y / mag }; // x / |x|, y / |y|
    }

    /*-----　演算子オーバーロード　-----*/

    // 逆ベクトル
    inline Vector2 operator -() const
    {
        return Vector2{ -this->x, -this->y };
    }

    // Vectorをそのまま足し合わせる
    inline Vector2 operator + () const
    {
        return *this;
    }

    Vector2& operator += (const Vector2 add_v2)
    {
        this->x += add_v2.x;
        this->y += add_v2.y;

        return *this; //*thisを返すことで v1 + v2 + v3見たく数珠繋ぎできる
    }

    Vector2& operator -= (const Vector2 minus_v2)
    {
        this->x -= minus_v2.x;
        this->y -= minus_v2.y;

        return *this;
    }

    Vector2& operator *= (float multiply_num)
    {
        this->x *= multiply_num;
        this->y *= multiply_num;

        return *this;
    }

    // 0.fで割ったときは±無限大を返す
    inline Vector2& operator /= (float divide_num)
    {
        if (divide_num == 0.0f) // 0で割ったら±無限大を返す
        {
            *this = Vector2{ ((this->x < 0) ? 1 : -1) * std::numeric_limits<float>::infinity(),
                            ((this->y < 0) ? 1 : -1) * std::numeric_limits<float>::infinity() };
            return *this;
        }

        this->x /= divide_num;
        this->y /= divide_num;

        return *this;
    }

    // 代入演算子 x,y,zを全部 change_numに変える
    Vector2& operator = (float change_num)
    {
        this->x = change_num;
        this->y = change_num;

        return *this;
    }

    // 一致演算子 x,y,zを全部一致するか一つでも違えばfalse
    bool operator == (const Vector2& v2_other)
    {
        if (this->x != v2_other.x) return false;
        if (this->y != v2_other.y) return false;
        return true;
    }

    // 不一致演算子一致演算子の逆
    bool operator != (const Vector2& v2_other)
    {
        return !(*this == v2_other);
    }
};

// Vector2どうしの足し算割り算掛け算割り算などの基本演算のグローバル定義

// Vector同士の足し算 x,y個別に足し合わせる
inline Vector2 operator + (const Vector2& left, const Vector2& right)
{
    Vector2 v2; //注意 vec1 = vec1 + vec2のとき vec1の数値が書き変わったら嫌だからv3を新たに用意
    v2.x = left.x + right.x; //[コレはダメ] left.x = left.x + right.x;
    v2.y = left.y + right.y;

    return v2;
}

// Vector同士の引き算 x,y個別に足し合わせる
inline Vector2 operator - (const Vector2& left, const Vector2& right)
{
    Vector2 v2; //注意 vec1 = vec1 - vec2のとき vec1の数値が書き変わったら嫌だからv2を新たに用意
    v2.x = left.x - right.x; //[コレはダメ] left.x = left.x - right.x;
    v2.y = left.y - right.y;

    return v2;
}

// Vectorと数値の掛け算 x,y個別に掛け合わせる
inline Vector2 operator * (const Vector2& left, float right)
{
    Vector2 v2;
    v2.x = left.x * right;
    v2.y = left.y * right;

    return v2;
}

// 数値とVectorの掛け算 x,y個別に掛け合わせる
inline Vector2 operator * (float left, const Vector2& right)
{
    Vector2 v2;
    v2.x = left * right.x;
    v2.y = left * right.y;

    return v2;
}

// Vectorと数値の割り算 x,y,z個別に割り合わせる
// 0.fで割ると±無限大を返す
inline Vector2 operator / (const Vector2& left, float right)
{
    if (right == 0.0f) // 0で割ったら±無限大を返す
        return Vector2{ ((left.x < 0) ? 1 : -1) * std::numeric_limits<float>::infinity(),
                        ((left.y < 0) ? 1 : -1) * std::numeric_limits<float>::infinity() };

    Vector2 v2;
    v2.x = left.x / right;
    v2.y = left.y / right;

    return v2;
}

// 比較不等号 < 演算子
inline bool operator < (const Vector2& left, const Vector2& right)
{
    if (left.x != right.x) return left.x < right.x;
    return left.y < right.y;
}

// 比較不等号 > 演算子
inline bool operator > (const Vector2& left, const Vector2& right)
{
    if (left.x != right.x) return left.x > right.x;
    return left.y > right.y;
}

// 比較不等号 <= 演算子
inline bool operator <= (const Vector2& left, const Vector2& right)
{
    return    !(left > right);
}

// 比較不等号 >= 演算子
inline bool operator >= (const Vector2& left, const Vector2& right)
{
    return    !(left < right);
}

// ベクトルの 2 乗の長さを返します(平方根しないぶん計算速い)
inline float sqrMagnitude(const Vector2& vec)
{
    return vec.x * vec.x + vec.y * vec.y; // x*x + y*y
}

// ベクトルの長さ(原点0から点(x,y)までの距離)
inline float magnitude(const Vector2& vec)
{
    return std::sqrt(sqrMagnitude(vec)); // √x*x + y*y
}

// 2つのベクトルの内積
inline float dot(const Vector2& left, const Vector2& right)
{
    return left.x * right.x + left.y * right.y; //普通にx同士,y同士掛けるだけ
}

// 2つのベクトルの外積
inline float cross(const Vector2& left, const Vector2& right)
{
    return left.x * right.y - left.y * right.x;// 外積のたすき掛け
}

#endif

MyMath.hを変更して円と線が接触しているか判定する関数CircleSegment関数を追加してみましょう。

#ifndef MYMATH_H_
#define MYMATH_H_

#include "Vector2.h" // 線との当たり判定にVector2を使う

#include <cmath>

// 数学関連クラス
class MyMath
{
public:
   static const float Sqrt2; // = 1.41421356237f;　// √2

   static const float PI; // = 3.14159265359f; // 円周率
   static const float Deg2Rad; // = PI / 180f; // 度からラジアンに変換する定数

    /// <summary>
    /// 円と円が重なっているかを調べる
    /// </summary>
    /// <param name="pc1">円1の中心pc1</param>
    /// <param name="radius1">円1の半径</param>
    /// <param name="pc2">円2の中心pc2</param>
    /// <param name="radius2">円2の半径</param>
    /// <returns>重なっていればtrue、重なっていなければfalseを返却する</returns>
    static bool CircleCircleIntersection(
        Vector2 pc1, float radius1,
        Vector2 pc2, float radius2)
    {
        return (pc1 - pc2).sqrMagnitude() < ((radius1 + radius2) * (radius1 + radius2));
    }

    /// <summary>
    /// 円と線が重なっているかを調べる
    /// </summary>
    /// <param name="pc">円の中心</param>
    /// <param name="r">円の半径</param>
    /// <param name="p1">線の端p1</param>
    /// <param name="p2">線の端p2</param>
    /// <returns>重なっていればtrue、重なっていなければfalseを返却する</returns>
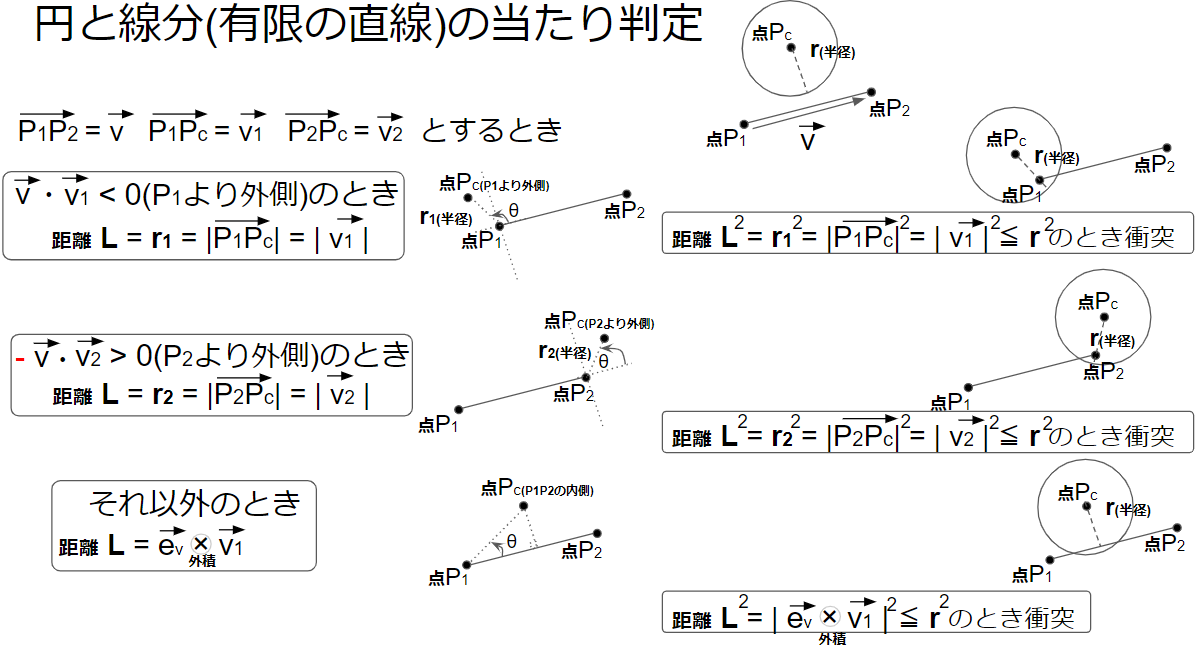
    static bool CircleSegment(Vector2 pc, float r, Vector2 p1, Vector2 p2)
    {
        Vector2 v12 = p2 - p1; // 線p1p2の始点p1から終点p2へ向かうベクトル
        Vector2 v1 = pc - p1; // 点p1から円の中心pcへ向かうベクトル
        Vector2 v2 = pc - p2; // 点p2から円の中心pcへ向かうベクトル
        Vector2 ev12 = v12.normalized(); // 単位ベクトル線p1p2のp1からp2へ向かう単位ベクトル
        float L; // 円と線の距離

        //円の中心pcが線p1p2の外側にあるかの判定のため内積を計算して線の外側の場合を考慮する
        if (dot(v12, v1) < 0) //点pcが線p1p2の外側にあるときは内積 < 0
            L = v1.magnitude(); //点pcと直線p1p2の距離は単なる直線距離でいい
        else if (dot(-v1, v2) < 0) //点pcが線p1p2の外側にあるときは内積 < 0
            L = v2.magnitude(); //点pcと直線p1p2の距離は単なる直線距離でいい
        else //外積を求めれば点pcと直線p1_p2の距離Lが求まる
            L = std::abs(cross(ev12, v1)); // |外積| (外積の絶対値をabsで求める)

        if (L < r) //衝突条件　L < r(L <= rにするかは地面から丁度半径r離れた位置で触れていると判定したいか次第)
            return true;
        else
            return false;
    }

};

#endif

下図で上記コードのv12をvに、ev12をevに置き換えて式との対応関係を確認してみてください。

main.cppを変更して円と線の当たり判定をしてみます。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p1{ 1,1 }; // (x,y) = (1,1)の位置の点
        Vector2 p2{ 7,13 }; // (x,y) = (7,13)の位置の点
        Vector2 p3{ 3,3 }; // (x,y) = (3,3)の位置の点
        float r = 1; // 円の半径

        Vector2 pc1{ 6,5 }; // 円1の中心
        float r1 = 2; // 円1の半径
        Vector2 pc2{ 8,9 }; // 円2の中心
        float r2 = 3; // 円1の半径

        Vector2 v13 = p3 - p1; // 終点p3 から始点p1を引くとp1からp3へ向かう方向ベクトルになる

        // 円1と円2が当たっているかの判定
        bool isCollision12 = MyMath::CircleCircleIntersection(pc1, r1, pc2, r2);

        // 円1と線p1p2が当たっているかの判定
        bool isCollision1_12 = MyMath::CircleSegment(pc1, r1, p1, p2);
        // 円2と線p1p2が当たっているかの判定
        bool isCollision2_12 = MyMath::CircleSegment(pc2, r2, p1, p2);

        mathGraph.DrawCircle(pc1.x, pc1.y, r1, (isCollision1_12) ? GetColor(255, 0, 0): GetColor(255, 255, 255), FALSE); // 円1を描く
        mathGraph.DrawCircle(pc2.x, pc2.y, r2, (isCollision2_12) ? GetColor(255, 0, 0) : GetColor(255, 255, 255), FALSE); // 円2を描く

        mathGraph.DrawLine(p1.x, p1.y, p2.x, p2.y, (isCollision1_12 || isCollision2_12) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分p1p2

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p0_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p0_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawLine(p1.x, p1.y, p1.x + Vector2::up.x * 3, p1.y + Vector2::up.y * 3, GetColor(0, 255, 255)); // upベクトルを3倍した線を描く

        mathGraph.DrawLine(p1.x, p1.y, p1.x + v13.x * 2, p1.y + v13.y * 2, GetColor(255, 0, 255)); // 線分p1p3の2倍した線を描く

        mathGraph.DrawLine(p1.x, p1.y, p1.x + v13.x, p1.y + v13.y, GetColor(255, 255, 255)); // 線分p1p3を描く

        mathGraph.DrawCircle(p3.x, p3.y, r, GetColor(0, 255, 0), FALSE); // 半径rの円(中心:p3)を描く(FALSEで塗りつぶし無し)

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかかでしょう? こんどは円1 と円2 と線分p1p2 の当たり判定をして、円2と線が接触して赤色になっていますか。
内積dotで (点p1→p2)・(点p1→円中心) < 0 以下なら内積のcosθが±90度を超えるので円の中心は線の外側p1サイドの外側になり、距離Lはmagnitudeで求まる
内積dotで (点p1←円中心)・(点p2→円中心) < 0 以下なら内積のcosθが±90度を超えるので円の中心は線の外側p2サイドの外側で、距離Lはmagnitudeで求まる
円の中心が線p1とp2の間の空中にあるのなら円と線の距離Lは外積=円の中心から線p1p2へ垂直に下した線の長さで求まる
というふうに内積dotで角度を判別して、大きさmagunitudeや外積crossと正規化normalizedの組み合わせで円と線の距離が求まっています。
ゲームの当たり判定に、内積dot、外積cross、大きさmagnitude、単位ベクトルnormalizedが活躍していることが実感できたでしょうか?

MyMathクラスで円と線が当たったら線に沿って押し戻す処理ができるようにする

MyMath.hを変更して円と線が接触したら押し戻した位置をreturnする関数CircleBoundを追加してみましょう。

#ifndef MYMATH_H_
#define MYMATH_H_

#include "Vector2.h" // 線との当たり判定にVector2を使う

#include <cmath>

// 数学関連クラス
class MyMath
{
public:
   static const float Sqrt2; // = 1.41421356237f;　// √2

   static const float PI; // = 3.14159265359f; // 円周率
   static const float Deg2Rad; // = PI / 180f; // 度からラジアンに変換する定数

    /// <summary>
    /// 円と円が重なっているかを調べる
    /// </summary>
    /// <param name="pc1">円1の中心pc1</param>
    /// <param name="radius1">円1の半径</param>
    /// <param name="pc2">円2の中心pc2</param>
    /// <param name="radius2">円2の半径</param>
    /// <returns>重なっていればtrue、重なっていなければfalseを返却する</returns>
    static bool CircleCircleIntersection(
        Vector2 pc1, float radius1,
        Vector2 pc2, float radius2)
    {
        return (pc1 - pc2).sqrMagnitude() < ((radius1 + radius2) * (radius1 + radius2));
    }

    /// <summary>
    /// 円と線が重なっているかを調べる
    /// </summary>
    /// <param name="pc">円の中心</param>
    /// <param name="r">円の半径</param>
    /// <param name="p1">線の端p1</param>
    /// <param name="p2">線の端p2</param>
    /// <returns>重なっていればtrue、重なっていなければfalseを返却する</returns>
    static bool CircleSegment(Vector2 pc, float r, Vector2 p1, Vector2 p2)
    {
        Vector2 v12 = p2 - p1; // 線p1p2の始点p1から終点p2へ向かうベクトル
        Vector2 v1 = pc - p1; // 点p1から円の中心pcへ向かうベクトル
        Vector2 v2 = pc - p2; // 点p2から円の中心pcへ向かうベクトル
        Vector2 ev12 = v12.normalized(); // 単位ベクトル線p1p2のp1からp2へ向かう単位ベクトル
        float L; // 円と線の距離

        //円の中心pcが線p1p2の外側にあるかの判定のため内積を計算して線の外側の場合を考慮する
        if (dot(v12, v1) < 0) //点pcが線p1p2の外側にあるときは内積 < 0
            L = v1.magnitude(); //点pcと直線p1p2の距離は単なる直線距離でいい
        else if (dot(-v1, v2) < 0) //点pcが線p1p2の外側にあるときは内積 < 0
            L = v2.magnitude(); //点pcと直線p1p2の距離は単なる直線距離でいい
        else //外積を求めれば点pcと直線p1_p2の距離Lが求まる
            L = std::abs(cross(ev12, v1)); // |外積| (外積の絶対値をabsで求める)

        if (L < r) //衝突条件　L < r(L <= rにするかは地面から丁度半径r離れた位置で触れていると判定したいか次第)
            return true;
        else
            return false;
    }

    /// <summary>
    /// 円と線が重なっているかを調べる
    /// </summary>
    /// <param name="pc">円の中心</param>
    /// <param name="r">円の半径</param>
    /// <param name="p1">線の端p1</param>
    /// <param name="p2">線の端p2</param>
    /// <returns>押し戻しした円の中心の点</returns>
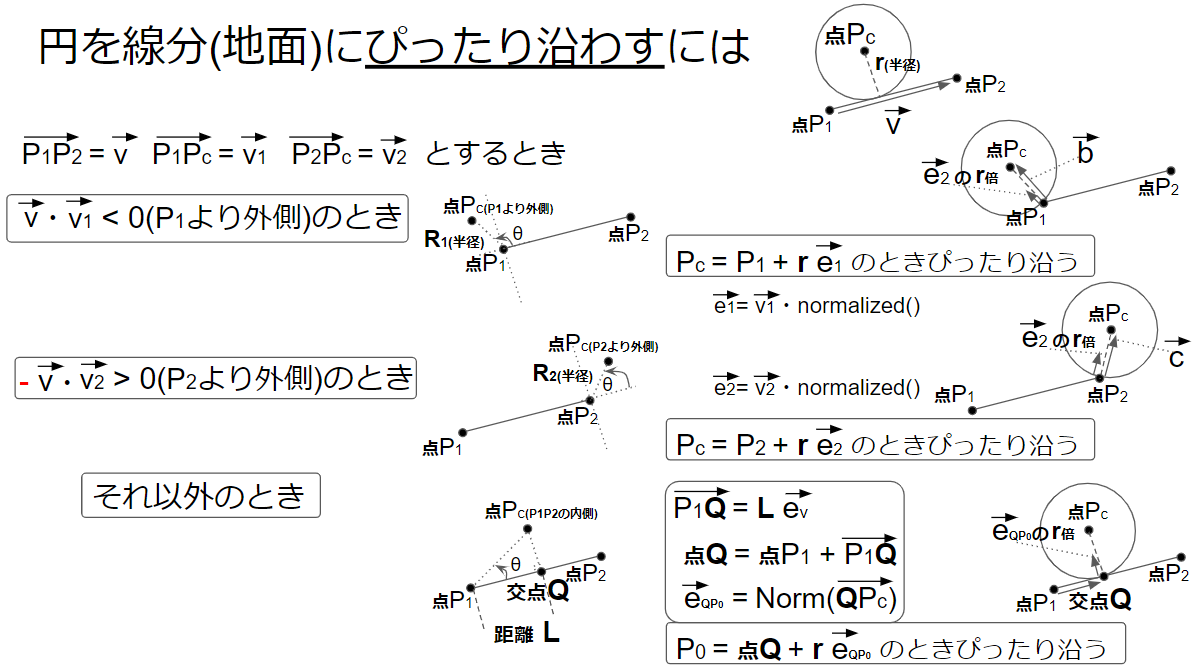
    static Vector2 CircleBound(Vector2 pc, float r, Vector2 p1, Vector2 p2)
    {
        Vector2 v12 = p2 - p1; // 線p1p2の始点p1から終点p2へ向かうベクトル
        Vector2 v1 = pc - p1; // 点p1から円の中心pcへ向かうベクトル
        Vector2 v2 = pc - p2; // 点p2から円の中心pcへ向かうベクトル
        Vector2 ev12 = v12.normalized(); // 単位ベクトル線p1p2のp1からp2へ向かう単位ベクトル

        //円の中心pcが線p1p2の外側にあるかの判定のため内積を計算して線の外側の場合を考慮する
        if (dot(v12, v1) < 0) //点pcが線p1p2の外側にあるときは内積 < 0
            return p1 + v1.normalized() * (r + 0.001f); // 半径よりちょっとだけ0.001f離れた位置まで押し戻す
        else if (dot(-v1, v2) < 0) //点p0が線p1p2の外側にあるときは内積 < 0
            return p2 + v2.normalized() * (r + 0.001f); // 半径よりちょっとだけ0.001f離れた位置まで押し戻す
        else //外積を求めれば点pcと直線p1_p2の距離Lが求まる
        {
            float L = dot(ev12, v1); // 内積で点p1から交点Qまでの距離を求める
            Vector2 Q = p1 + L * ev12; // 円と線の衝突点Q
            Vector2 e = (pc - Q).normalized(); // 跳ね返り方向のの半径1の単位ベクトル
            return Q + e * (r + 0.001f); // 押し戻し処理
        }
    }

};

#endif

下図で上記コードのv12をvに、ev12をevに置き換えて式との対応関係を確認してみてください。

main.cppを変更して円と線の当たり判定をして接触している際はMyMath::CircleBoundで円を押し戻した位置を描く処理を追加してみます。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p1{ 1,1 }; // (x,y) = (1,1)の位置の点
        Vector2 p2{ 8,8 }; // (x,y) = (8,8)の位置の点
        Vector2 p3{ 3,3 }; // (x,y) = (3,3)の位置の点
        float r = 1; // 円の半径

        Vector2 pc1{ 6,5 }; // 円1の中心
        float r1 = 2; // 円1の半径
        Vector2 pc2{ 8,9 }; // 円2の中心
        float r2 = 3; // 円1の半径

        Vector2 v13 = p3 - p1; // 終点p3 から始点p1を引くとp1からp3へ向かう方向ベクトルになる

        // 円1と円2が当たっているかの判定
        bool isCollision12 = MyMath::CircleCircleIntersection(pc1, r1, pc2, r2);

        // 円1と線p1p2が当たっているかの判定
        bool isCollision1_12 = MyMath::CircleSegment(pc1, r1, p1, p2);
        // 円2と線p1p2が当たっているかの判定
        bool isCollision2_12 = MyMath::CircleSegment(pc2, r2, p1, p2);

        Vector2 pb1 = pc1; // 線に押し戻された円1の中心
        if (isCollision1_12)
            pb1 = MyMath::CircleBound(pc1, r1, p1, p2);

        Vector2 pb2 = pc2; // 線に押し戻された円2の中心
        if (isCollision2_12)
            pb2 = MyMath::CircleBound(pc2, r2, p1, p2);

        mathGraph.DrawCircle(pc1.x, pc1.y, r1, (isCollision1_12) ? GetColor(255, 0, 0): GetColor(255, 255, 255), FALSE); // 円1を描く
        mathGraph.DrawCircle(pc2.x, pc2.y, r2, (isCollision2_12) ? GetColor(255, 0, 0) : GetColor(255, 255, 255), FALSE); // 円2を描く

        if (pb1 != pc1) // 線に当たって押し戻された円1を描く
            mathGraph.DrawCircle(pb1.x, pb1.y, r1, GetColor(255, 0, 255), FALSE);
        if (pb2 != pc2) // 線に当たって押し戻された円2を描く
            mathGraph.DrawCircle(pb2.x, pb2.y, r2, GetColor(255, 0, 255), FALSE);

        mathGraph.DrawLine(p1.x, p1.y, p2.x, p2.y, (isCollision1_12 || isCollision2_12) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分p1p2

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p0_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p0_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawLine(p1.x, p1.y, p1.x + Vector2::up.x * 3, p1.y + Vector2::up.y * 3, GetColor(0, 255, 255)); // upベクトルを3倍した線を描く

        mathGraph.DrawLine(p1.x, p1.y, p1.x + v13.x * 2, p1.y + v13.y * 2, GetColor(255, 0, 255)); // 線分p1p3の2倍した線を描く

        mathGraph.DrawLine(p1.x, p1.y, p1.x + v13.x, p1.y + v13.y, GetColor(255, 255, 255)); // 線分p1p3を描く

        mathGraph.DrawCircle(p3.x, p3.y, r, GetColor(0, 255, 0), FALSE); // 半径rの円(中心:p3)を描く(FALSEで塗りつぶし無し)

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかかでしょう? 線と円1 と円2 の両方が接触して押し戻されて線にぴったり沿う位置に円が描かれていますか。

MyMathクラスで線に垂直に下した点の影(射影)位置と線と点の最短距離を求める

MyMath.hを変更して線p1p2に対して点p0から垂直に下した交点Qとp0からQへの距離Lと点p0から線p1p2への最短距離Hを求める関数LineProjectionを追加してみましょう。

#ifndef MYMATH_H_
#define MYMATH_H_

#include "Vector2.h" // 線との当たり判定にVector2を使う

#include <cmath>

// 数学関連クラス
class MyMath
{
public:
   static const float Sqrt2; // = 1.41421356237f;　// √2

   static const float PI; // = 3.14159265359f; // 円周率
   static const float Deg2Rad; // = PI / 180f; // 度からラジアンに変換する定数

    /// <summary>
    /// 円と円が重なっているかを調べる
    /// </summary>
    /// <param name="pc1">円1の中心pc1</param>
    /// <param name="radius1">円1の半径</param>
    /// <param name="pc2">円2の中心pc2</param>
    /// <param name="radius2">円2の半径</param>
    /// <returns>重なっていればtrue、重なっていなければfalseを返却する</returns>
    static bool CircleCircleIntersection(
        Vector2 pc1, float radius1,
        Vector2 pc2, float radius2)
    {
        return (pc1 - pc2).sqrMagnitude() < ((radius1 + radius2) * (radius1 + radius2));
    }

    /// <summary>
    /// 円と線が重なっているかを調べる
    /// </summary>
    /// <param name="pc">円の中心</param>
    /// <param name="r">円の半径</param>
    /// <param name="p1">線の端p1</param>
    /// <param name="p2">線の端p2</param>
    /// <returns>重なっていればtrue、重なっていなければfalseを返却する</returns>
    static bool CircleSegment(Vector2 pc, float r, Vector2 p1, Vector2 p2)
    {
        Vector2 v12 = p2 - p1; // 線p1p2の始点p1から終点p2へ向かうベクトル
        Vector2 v1 = pc - p1; // 点p1から円の中心pcへ向かうベクトル
        Vector2 v2 = pc - p2; // 点p2から円の中心pcへ向かうベクトル
        Vector2 ev12 = v12.normalized(); // 単位ベクトル線p1p2のp1からp2へ向かう単位ベクトル
        float L; // 円と線の距離

        //円の中心pcが線p1p2の外側にあるかの判定のため内積を計算して線の外側の場合を考慮する
        if (dot(v12, v1) < 0) //点pcが線p1p2の外側にあるときは内積 < 0
            L = v1.magnitude(); //点pcと直線p1p2の距離は単なる直線距離でいい
        else if (dot(-v1, v2) < 0) //点pcが線p1p2の外側にあるときは内積 < 0
            L = v2.magnitude(); //点pcと直線p1p2の距離は単なる直線距離でいい
        else //外積を求めれば点pcと直線p1_p2の距離Lが求まる
            L = std::abs(cross(ev12, v1)); // |外積| (外積の絶対値をabsで求める)

        if (L < r) //衝突条件　L < r(L <= rにするかは地面から丁度半径r離れた位置で触れていると判定したいか次第)
            return true;
        else
            return false;
    }

    /// <summary>
    /// 円と線が重なっているかを調べる
    /// </summary>
    /// <param name="pc">円の中心</param>
    /// <param name="r">円の半径</param>
    /// <param name="p1">線の端p1</param>
    /// <param name="p2">線の端p2</param>
    /// <returns>押し戻しした円の中心の点</returns>
    static Vector2 CircleBound(Vector2 pc, float r, Vector2 p1, Vector2 p2)
    {
        Vector2 v12 = p2 - p1; // 線p1p2の始点p1から終点p2へ向かうベクトル
        Vector2 v1 = pc - p1; // 点p1から円の中心pcへ向かうベクトル
        Vector2 v2 = pc - p2; // 点p2から円の中心pcへ向かうベクトル
        Vector2 ev12 = v12.normalized(); // 単位ベクトル線p1p2のp1からp2へ向かう単位ベクトル

        //円の中心pcが線p1p2の外側にあるかの判定のため内積を計算して線の外側の場合を考慮する
        if (dot(v12, v1) < 0) //点pcが線p1p2の外側にあるときは内積 < 0
            return p1 + v1.normalized() * (r + 0.001f); // 半径よりちょっとだけ0.001f離れた位置まで押し戻す
        else if (dot(-v1, v2) < 0) //点p0が線p1p2の外側にあるときは内積 < 0
            return p2 + v2.normalized() * (r + 0.001f); // 半径よりちょっとだけ0.001f離れた位置まで押し戻す
        else //外積を求めれば点pcと直線p1_p2の距離Lが求まる
        {
            float L = dot(ev12, v1); // 内積で点p1から交点Qまでの距離を求める
            Vector2 Q = p1 + L * ev12; // 円と線の衝突点Q
            Vector2 e = (pc - Q).normalized(); // 跳ね返り方向のの半径1の単位ベクトル
            return Q + e * (r + 0.001f); // 押し戻し処理
        }
    }


    /// <summary>
    /// 斜面a(線p1→p2),線b(p1→p0)のとき斜面a上に点p0から垂直に下した射影点(点Q)の位置とp0からQへの長さLとp0と線aとの距離Hを求める
    /// </summary>
    /// <param name="p0">線bの先っぽp0</param>
    /// <param name="p1">aとbの起点p1</param>
    /// <param name="p2">斜面aの端p2</param>
    /// <param name="L">p1からQまでの距離</param>
    /// <param name="H">p0と直線p1p2の距離(= 高さ[線の内側]か端っこの点からの半径[線の外側])</param>
    /// <returns>線aに線bから下した交点Q</returns>
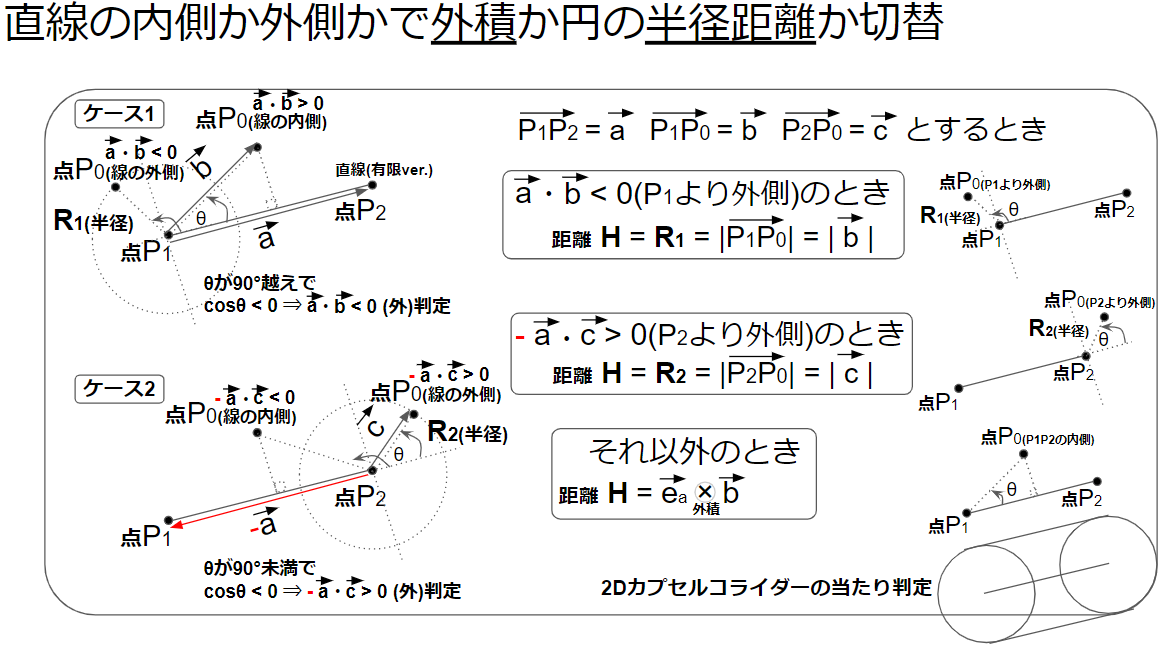
    static Vector2 LineProjection(Vector2 p0, Vector2 p1, Vector2 p2, float& L, float& H, Vector2& nearest)
    {
        // ベクトルaとベクトルbを求める。ただマイナスするだけ。
        Vector2 a = p2 - p1;
        Vector2 b = p0 - p1;
        Vector2 c = p0 - p2; // p2→p0のベクトル
        // 正規化ベクトルを求める
        Vector2 ea = a.normalized(); // a / |a|
        bool isOutside = false; // p0が線の外側か?

        //点p0が線p1p2の外側にあるかの判定のため内積を計算して線の外側の場合を考慮する
        if (dot(a, b) < 0) // 点p0が線p1p2の外側にあるときは内積 < 0
        {
            H = b.magnitude(); // 点p0と直線p1p2の距離は単なるベクトルbの直線距離でいい
            nearest = p1; // 一番近い点はp1
            isOutside = true; // p1側の外側
        }
        else if (dot(-a, c) < 0) // 点p0が線p1p2の外側にあるときは内積 < 0
        {
            H = c.magnitude(); // 点p0と直線p1p2の距離は単なるベクトルcの直線距離でいい
            nearest = p2; // 一番近い点はp2
            isOutside = true; // p2側の外側
        }
        else
        {   // 外積を求めれば点p0と直線p1_p2の距離Lが求まる
            Vector2 ea_cross_b = cross(ea, b);
            H = ea_cross_b.magnitude();
        }

        L = dot(ea, b); // 長さLは内積で求まる
        Vector2 resultQ = p1 + L * ea;

        if (!isOutside)
            nearest = resultQ; // 一番近い点はQ

        return resultQ;
    }

};

#endif

下図で上記コードの式との対応関係を確認してみてください。

main.cppがちらかってきたので一旦、今まで書いてきたVector関連のコードを消してから今回のコードを入れましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p1{ 1,1 }; // (x,y) = (1,1)の位置の点
        Vector2 p2{ 8,8 }; // (x,y) = (8,8)の位置の点
        Vector2 p3{ 3,3 }; // (x,y) = (3,3)の位置の点
        float r = 1; // 円の半径

        Vector2 pc1{ 6,5 }; // 円1の中心
        float r1 = 2; // 円1の半径
        Vector2 pc2{ 8,9 }; // 円2の中心
        float r2 = 3; // 円1の半径

        Vector2 v13 = p3 - p1; // 終点p3 から始点p1を引くとp1からp3へ向かう方向ベクトルになる

        // 円1と円2が当たっているかの判定
        bool isCollision12 = MyMath::CircleCircleIntersection(pc1, r1, pc2, r2);

        // 円1と線p1p2が当たっているかの判定
        bool isCollision1_12 = MyMath::CircleSegment(pc1, r1, p1, p2);
        // 円2と線p1p2が当たっているかの判定
        bool isCollision2_12 = MyMath::CircleSegment(pc2, r2, p1, p2);

        Vector2 pb1 = pc1; // 線に押し戻された円1の中心
        if (isCollision1_12)
            pb1 = MyMath::CircleBound(pc1, r1, p1, p2);

        Vector2 pb2 = pc2; // 線に押し戻された円2の中心
        if (isCollision2_12)
            pb2 = MyMath::CircleBound(pc2, r2, p1, p2);

        mathGraph.DrawCircle(pc1.x, pc1.y, r1, (isCollision1_12) ? GetColor(255, 0, 0): GetColor(255, 255, 255), FALSE); // 円1を描く
        mathGraph.DrawCircle(pc2.x, pc2.y, r2, (isCollision2_12) ? GetColor(255, 0, 0) : GetColor(255, 255, 255), FALSE); // 円2を描く

        if (pb1 != pc1) // 線に当たって押し戻された円1を描く
            mathGraph.DrawCircle(pb1.x, pb1.y, r1, GetColor(255, 0, 255), FALSE);
        if (pb2 != pc2) // 線に当たって押し戻された円2を描く
            mathGraph.DrawCircle(pb2.x, pb2.y, r2, GetColor(255, 0, 255), FALSE);

        mathGraph.DrawLine(p1.x, p1.y, p2.x, p2.y, (isCollision1_12 || isCollision2_12) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分p1p2

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p0_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p0_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawLine(p1.x, p1.y, p1.x + Vector2::up.x * 3, p1.y + Vector2::up.y * 3, GetColor(0, 255, 255)); // upベクトルを3倍した線を描く

        mathGraph.DrawLine(p1.x, p1.y, p1.x + v13.x * 2, p1.y + v13.y * 2, GetColor(255, 0, 255)); // 線分p1p3の2倍した線を描く

        mathGraph.DrawLine(p1.x, p1.y, p1.x + v13.x, p1.y + v13.y, GetColor(255, 255, 255)); // 線分p1p3を描く

        mathGraph.DrawCircle(p3.x, p3.y, r, GetColor(0, 255, 0), FALSE); // 半径rの円(中心:p3)を描く(FALSEで塗りつぶし無し)

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

main.cppを変更してMyMath::LineProjectionで線に点から垂直に下した位置と最短距離の表示処理を追加してみます。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p0{ 5,8 };
        Vector2 p1{ 2,2 };
        Vector2 p2{ 10,3 };

        float L = 0; // 点p1から交点Qへの距離
        float H = 0; // 線分p1p2と点p0の最短距離H
        Vector2 nearest; // 点p0から一番近い直線p1p2上の点
        Vector2 Q = MyMath::LineProjection(p0,p1,p2,L,H, nearest); // 点p0から線分p1p2に垂直に下した交点Q

        mathGraph.DrawLine(p1.x, p1.y, p2.x, p2.y, GetColor(255, 255, 255)); // 線分p1p2
        mathGraph.DrawLine(p1.x, p1.y, p0.x, p0.y, GetColor(150, 150, 150)); // 線分p1p0

        mathGraph.DrawLine(p0.x, p0.y, nearest.x, nearest.y, GetColor(255, 255, 0)); // p0からの最短距離を描く
        mathGraph.DrawLine(p1.x, p1.y, Q.x, Q.y, GetColor(0, 255, 255)); // p0からQへの距離Lを描く

        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(Q.x, Q.y, 3, GetColor(255, 0, 255), TRUE);
        std::string Q_String = "Q=(" + std::to_string(Q.x) + "," + std::to_string(Q.y) + ")";
        mathGraph.DrawString(Q.x, Q.y-5, Q_String.c_str(), GetColor(255, 0, 255));

        std::string H_String = "最短距離H=" + std::to_string(H);
        mathGraph.DrawString(nearest.x, nearest.y - 10, H_String.c_str(), GetColor(255, 255, 0));

        std::string L_String = "L=" + std::to_string(L);
        mathGraph.DrawString(Q.x, Q.y - 3, L_String.c_str(), GetColor(0, 255, 255));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがですか？最短距離が表示されましたか?
念のため、p1側の外側の場合の最短距離も試しておきましょう。

main.cppの数値を変更してp1側の外側の場合の最短距離も試しておきましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p0{ -3,8 };
        Vector2 p1{ 2,2 };
        Vector2 p2{ 10,3 };

        float L = 0; // 点p1から交点Qへの距離
        float H = 0; // 線分p1p2と点p0の最短距離H
        Vector2 nearest; // 点p0から一番近い直線p1p2上の点
        Vector2 Q = MyMath::LineProjection(p0,p1,p2,L,H, nearest); // 点p0から線分p1p2に垂直に下した交点Q

        mathGraph.DrawLine(p1.x, p1.y, p2.x, p2.y, GetColor(255, 255, 255)); // 線分p1p2
        mathGraph.DrawLine(p1.x, p1.y, p0.x, p0.y, GetColor(150, 150, 150)); // 線分p1p0

        mathGraph.DrawLine(p0.x, p0.y, nearest.x, nearest.y, GetColor(255, 255, 0)); // p0からの最短距離を描く
        mathGraph.DrawLine(p1.x, p1.y, Q.x, Q.y, GetColor(0, 255, 255)); // p0からQへの距離Lを描く

        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(Q.x, Q.y, 3, GetColor(255, 0, 255), TRUE);
        std::string Q_String = "Q=(" + std::to_string(Q.x) + "," + std::to_string(Q.y) + ")";
        mathGraph.DrawString(Q.x, Q.y-5, Q_String.c_str(), GetColor(255, 0, 255));

        std::string H_String = "最短距離H=" + std::to_string(H);
        mathGraph.DrawString(nearest.x, nearest.y - 10, H_String.c_str(), GetColor(255, 255, 0));

        std::string L_String = "L=" + std::to_string(L);
        mathGraph.DrawString(Q.x, Q.y - 3, L_String.c_str(), GetColor(0, 255, 255));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがですか？p1側の外側の場合の最短距離が表示されましたか?
念のため、p2側の外側の場合の最短距離も試しておきましょう。

main.cppの数値を変更してp2側の外側の場合の最短距離も試しておきましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p0{ 15,8 };
        Vector2 p1{ 2,2 };
        Vector2 p2{ 10,3 };

        float L = 0; // 点p1から交点Qへの距離
        float H = 0; // 線分p1p2と点p0の最短距離H
        Vector2 nearest; // 点p0から一番近い直線p1p2上の点
        Vector2 Q = MyMath::LineProjection(p0,p1,p2,L,H, nearest); // 点p0から線分p1p2に垂直に下した交点Q

        mathGraph.DrawLine(p1.x, p1.y, p2.x, p2.y, GetColor(255, 255, 255)); // 線分p1p2
        mathGraph.DrawLine(p1.x, p1.y, p0.x, p0.y, GetColor(150, 150, 150)); // 線分p1p0

        mathGraph.DrawLine(p0.x, p0.y, nearest.x, nearest.y, GetColor(255, 255, 0)); // p0からの最短距離を描く
        mathGraph.DrawLine(p1.x, p1.y, Q.x, Q.y, GetColor(0, 255, 255)); // p0からQへの距離Lを描く

        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(Q.x, Q.y, 3, GetColor(255, 0, 255), TRUE);
        std::string Q_String = "Q=(" + std::to_string(Q.x) + "," + std::to_string(Q.y) + ")";
        mathGraph.DrawString(Q.x, Q.y-5, Q_String.c_str(), GetColor(255, 0, 255));

        std::string H_String = "最短距離H=" + std::to_string(H);
        mathGraph.DrawString(nearest.x, nearest.y - 10, H_String.c_str(), GetColor(255, 255, 0));

        std::string L_String = "L=" + std::to_string(L);
        mathGraph.DrawString(Q.x, Q.y - 3, L_String.c_str(), GetColor(0, 255, 255));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょうか？この最短距離の処理は2Dのカプセルコライダーの点との当たり判定の場合分けの条件と同じです。
カプセルコライダーは複雑そうに思えて、実はシンプルな内積や外積の場合分けの計算で高速に計算できるのです。
計算時間が早く、当たり判定の伸縮性がありゲームの当たり判定はカプセルコライダーを多用して制作されているのです。

MyMathクラスで線と線が交差するか判定する

MyMath.hを変更して線分line0と線分line1が交差するかを求める関数LineIntersection(判定のみ ver.)を追加してみましょう。

#ifndef MYMATH_H_
#define MYMATH_H_

#include "Vector2.h" // 線との当たり判定にVector2を使う

#include <cmath>

// 数学関連クラス
class MyMath
{
public:
   static const float Sqrt2; // = 1.41421356237f;　// √2

   static const float PI; // = 3.14159265359f; // 円周率
   static const float Deg2Rad; // = PI / 180f; // 度からラジアンに変換する定数

    /// <summary>
    /// 円と円が重なっているかを調べる
    /// </summary>
    /// <param name="pc1">円1の中心pc1</param>
    /// <param name="radius1">円1の半径</param>
    /// <param name="pc2">円2の中心pc2</param>
    /// <param name="radius2">円2の半径</param>
    /// <returns>重なっていればtrue、重なっていなければfalseを返却する</returns>
    static bool CircleCircleIntersection(
        Vector2 pc1, float radius1,
        Vector2 pc2, float radius2)
    {
        return (pc1 - pc2).sqrMagnitude() < ((radius1 + radius2) * (radius1 + radius2));
    }

    /// <summary>
    /// 円と線が重なっているかを調べる
    /// </summary>
    /// <param name="pc">円の中心</param>
    /// <param name="r">円の半径</param>
    /// <param name="p1">線の端p1</param>
    /// <param name="p2">線の端p2</param>
    /// <returns>重なっていればtrue、重なっていなければfalseを返却する</returns>
    static bool CircleSegment(Vector2 pc, float r, Vector2 p1, Vector2 p2)
    {
        Vector2 v12 = p2 - p1; // 線p1p2の始点p1から終点p2へ向かうベクトル
        Vector2 v1 = pc - p1; // 点p1から円の中心pcへ向かうベクトル
        Vector2 v2 = pc - p2; // 点p2から円の中心pcへ向かうベクトル
        Vector2 ev12 = v12.normalized(); // 単位ベクトル線p1p2のp1からp2へ向かう単位ベクトル
        float L; // 円と線の距離

        //円の中心pcが線p1p2の外側にあるかの判定のため内積を計算して線の外側の場合を考慮する
        if (dot(v12, v1) < 0) //点pcが線p1p2の外側にあるときは内積 < 0
            L = v1.magnitude(); //点pcと直線p1p2の距離は単なる直線距離でいい
        else if (dot(-v1, v2) < 0) //点pcが線p1p2の外側にあるときは内積 < 0
            L = v2.magnitude(); //点pcと直線p1p2の距離は単なる直線距離でいい
        else //外積を求めれば点pcと直線p1_p2の距離Lが求まる
            L = std::abs(cross(ev12, v1)); // |外積| (外積の絶対値をabsで求める)

        if (L < r) //衝突条件　L < r(L <= rにするかは地面から丁度半径r離れた位置で触れていると判定したいか次第)
            return true;
        else
            return false;
    }

    /// <summary>
    /// 円と線が重なっているかを調べる
    /// </summary>
    /// <param name="pc">円の中心</param>
    /// <param name="r">円の半径</param>
    /// <param name="p1">線の端p1</param>
    /// <param name="p2">線の端p2</param>
    /// <returns>押し戻しした円の中心の点</returns>
    static Vector2 CircleBound(Vector2 pc, float r, Vector2 p1, Vector2 p2)
    {
        Vector2 v12 = p2 - p1; // 線p1p2の始点p1から終点p2へ向かうベクトル
        Vector2 v1 = pc - p1; // 点p1から円の中心pcへ向かうベクトル
        Vector2 v2 = pc - p2; // 点p2から円の中心pcへ向かうベクトル
        Vector2 ev12 = v12.normalized(); // 単位ベクトル線p1p2のp1からp2へ向かう単位ベクトル

        //円の中心pcが線p1p2の外側にあるかの判定のため内積を計算して線の外側の場合を考慮する
        if (dot(v12, v1) < 0) //点pcが線p1p2の外側にあるときは内積 < 0
            return p1 + v1.normalized() * (r + 0.001f); // 半径よりちょっとだけ0.001f離れた位置まで押し戻す
        else if (dot(-v1, v2) < 0) //点p0が線p1p2の外側にあるときは内積 < 0
            return p2 + v2.normalized() * (r + 0.001f); // 半径よりちょっとだけ0.001f離れた位置まで押し戻す
        else //外積を求めれば点pcと直線p1_p2の距離Lが求まる
        {
            float L = dot(ev12, v1); // 内積で点p1から交点Qまでの距離を求める
            Vector2 Q = p1 + L * ev12; // 円と線の衝突点Q
            Vector2 e = (pc - Q).normalized(); // 跳ね返り方向のの半径1の単位ベクトル
            return Q + e * (r + 0.001f); // 押し戻し処理
        }
    }


    /// <summary>
    /// 斜面a(線p1→p2),線b(p1→p0)のとき斜面a上に点p0から垂直に下した射影点(点Q)の位置とp0からQへの長さLとp0と線aとの距離Hを求める
    /// </summary>
    /// <param name="p0">線bの先っぽp0</param>
    /// <param name="p1">aとbの起点p1</param>
    /// <param name="p2">斜面aの端p2</param>
    /// <param name="L">p1からQまでの距離</param>
    /// <param name="H">p0と直線p1p2の距離(= 高さ[線の内側]か端っこの点からの半径[線の外側])</param>
    /// <returns>線aに線bから下した交点Q</returns>
    static Vector2 LineProjection(Vector2 p0, Vector2 p1, Vector2 p2, float& L, float& H, Vector2& nearest)
    {
        // ベクトルaとベクトルbを求める。ただマイナスするだけ。
        Vector2 a = p2 - p1;
        Vector2 b = p0 - p1;
        Vector2 c = p0 - p2; // p2→p0のベクトル
        // 正規化ベクトルを求める
        Vector2 ea = a.normalized(); // a / |a|
        bool isOutside = false; // p0が線の外側か?

        //点p0が線p1p2の外側にあるかの判定のため内積を計算して線の外側の場合を考慮する
        if (dot(a, b) < 0) // 点p0が線p1p2の外側にあるときは内積 < 0
        {
            H = b.magnitude(); // 点p0と直線p1p2の距離は単なるベクトルbの直線距離でいい
            nearest = p1; // 一番近い点はp1
            isOutside = true; // p1側の外側
        }
        else if (dot(-a, c) < 0) // 点p0が線p1p2の外側にあるときは内積 < 0
        {
            H = c.magnitude(); // 点p0と直線p1p2の距離は単なるベクトルcの直線距離でいい
            nearest = p2; // 一番近い点はp2
            isOutside = true; // p2側の外側
        }
        else
        {   // 外積を求めれば点p0と直線p1_p2の距離Lが求まる
            Vector2 ea_cross_b = cross(ea, b);
            H = ea_cross_b.magnitude();
        }

        L = dot(ea, b); // 長さLは内積で求まる
        Vector2 resultQ = p1 + L * ea;

        if (!isOutside)
            nearest = resultQ; // 一番近い点はQ

        return resultQ;
    }

    /// <summary>
    /// 線line0と線line1が重なっているかを調べる
    /// </summary>
    /// <param name="line0start">線line0の始点</param>
    /// <param name="line0end">線line0の終点</param>
    /// <param name="line1start">線line1の始点</param>
    /// <param name="line1end">線line1の終点</param>
    /// <returns>線line0と線line1が交差しているならtrue,してないならfalse</returns>
    static bool LineIntersection(Vector2 line0start, Vector2 line0end, Vector2 line1start, Vector2 line1end)
    {
        Vector2 v0 = line0end - line0start; // line0の始点startから終点endへのベクトル
        Vector2 v1 = line1end - line1start; // line1の始点startから終点endへのベクトル
        Vector2 v01 = line1start - line0start; // line0の始点からline1の始点へのベクトル 0start→1start
        float t1 = cross(v01, v0) / cross(v0, v1);
        float t0 = cross(v01, v1) / cross(v0, v1);

        // 線分line0と線分line1が【交差しているか判定】
        if (0 < t1 && t1 < 1 && 0 < t0 && t0 < 1) return true; //【交差している】

        return false; // 線分line0と線分line1は【交差していない】
    }

};

#endif

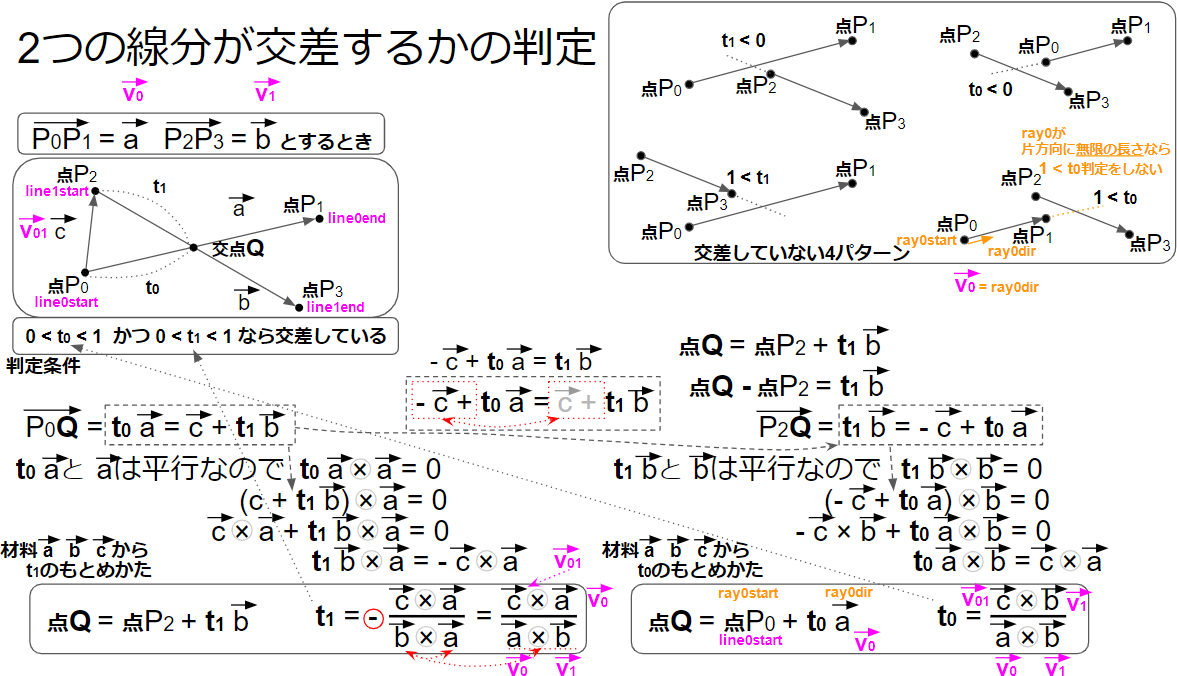
下図で上記コードの式との対応関係を確認してみてください。(ベクトルaをv0にベクトルbをv1にベクトルcをv01に置き換えてみよう[ピンクの部分])

main.cppがちらかってきたので一旦、今まで書いてきたVector関連のコードを消してから今回のコードを入れましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p0{ 15,8 };
        Vector2 p1{ 2,2 };
        Vector2 p2{ 10,3 };

        float L = 0; // 点p1から交点Qへの距離
        float H = 0; // 線分p1p2と点p0の最短距離H
        Vector2 nearest; // 点p0から一番近い直線p1p2上の点
        Vector2 Q = MyMath::LineProjection(p0,p1,p2,L,H, nearest); // 点p0から線分p1p2に垂直に下した交点Q

        mathGraph.DrawLine(p1.x, p1.y, p2.x, p2.y, GetColor(255, 255, 255)); // 線分p1p2
        mathGraph.DrawLine(p1.x, p1.y, p0.x, p0.y, GetColor(150, 150, 150)); // 線分p1p0

        mathGraph.DrawLine(p0.x, p0.y, nearest.x, nearest.y, GetColor(255, 255, 0)); // p0からの最短距離を描く
        mathGraph.DrawLine(p1.x, p1.y, Q.x, Q.y, GetColor(0, 255, 255)); // p0からQへの距離Lを描く

        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(Q.x, Q.y, 3, GetColor(255, 0, 255), TRUE);
        std::string Q_String = "Q=(" + std::to_string(Q.x) + "," + std::to_string(Q.y) + ")";
        mathGraph.DrawString(Q.x, Q.y-5, Q_String.c_str(), GetColor(255, 0, 255));

        std::string H_String = "最短距離H=" + std::to_string(H);
        mathGraph.DrawString(nearest.x, nearest.y - 10, H_String.c_str(), GetColor(255, 255, 0));

        std::string L_String = "L=" + std::to_string(L);
        mathGraph.DrawString(Q.x, Q.y - 3, L_String.c_str(), GetColor(0, 255, 255));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

main.cppを変更してMyMath::LineIntersectionで線分line0と線分line1が交差するかの判定を追加してみます。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // 線分line0
        Vector2 p0{ 5,5 };
        Vector2 p1{ 15,11 };
        // 線分line1
        Vector2 p2{ 5,10 };
        Vector2 p3{ 15,6 };

        bool isCollision01 = MyMath::LineIntersection(p0, p1, p2, p3);

        mathGraph.DrawArrow(p0.x, p0.y, 0, 0, p1.x, p1.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line0
        mathGraph.DrawArrow(p2.x, p2.y, 0, 0, p3.x, p3.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line1

        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(p3.x, p3.y, 3, GetColor(0, 255, 255), TRUE);
        std::string p3_String = "p3=(" + std::to_string((int)p3.x) + "," + std::to_string((int)p3.y) + ")";
        mathGraph.DrawString(p3.x, p3.y, p3_String.c_str(), GetColor(0, 255, 255));


        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがですか？線line0と線line1が交差しているので線が赤色で表示されましたか?
念のため、交差しない場合も試しておきましょう。

main.cppの点p1の位置を変更して線分line0と線分line1が交差しない場合(t0 < 0)の判定を試してみます。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // 線分line0
        Vector2 p0{ 11,9 };
        Vector2 p1{ 15,11 };
        // 線分line1
        Vector2 p2{ 5,10 };
        Vector2 p3{ 15,6 };

        bool isCollision01 = MyMath::LineIntersection(p0, p1, p2, p3);

        mathGraph.DrawArrow(p0.x, p0.y, 0, 0, p1.x, p1.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line0
        mathGraph.DrawArrow(p2.x, p2.y, 0, 0, p3.x, p3.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line1

        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(p3.x, p3.y, 3, GetColor(0, 255, 255), TRUE);
        std::string p3_String = "p3=(" + std::to_string((int)p3.x) + "," + std::to_string((int)p3.y) + ")";
        mathGraph.DrawString(p3.x, p3.y, p3_String.c_str(), GetColor(0, 255, 255));


        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがですか？線line0と線line1が交差していていない(t0 < 0)ので線が白色で表示されましたか?
念のため、別の交差しない場合(1 < t0のとき)も試しておきましょう。

main.cppの点p1の位置を変更して線分line0と線分line1が交差しない場合(1 < t0)の判定を試してみます。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // 線分line0
        Vector2 p0{ 5,5 };
        Vector2 p1{ 9,7 };
        // 線分line1
        Vector2 p2{ 5,10 };
        Vector2 p3{ 15,6 };

        bool isCollision01 = MyMath::LineIntersection(p0, p1, p2, p3);

        mathGraph.DrawArrow(p0.x, p0.y, 0, 0, p1.x, p1.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line0
        mathGraph.DrawArrow(p2.x, p2.y, 0, 0, p3.x, p3.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line1

        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(p3.x, p3.y, 3, GetColor(0, 255, 255), TRUE);
        std::string p3_String = "p3=(" + std::to_string((int)p3.x) + "," + std::to_string((int)p3.y) + ")";
        mathGraph.DrawString(p3.x, p3.y, p3_String.c_str(), GetColor(0, 255, 255));


        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがですか？線line0と線line1が交差していていない(1 < t0)ので線が白色で表示されましたか?
念のため、別の交差しない場合(t1 < 0のとき)も試しておきましょう。

main.cppの点p1の位置を変更して線分line0と線分line1が交差しない場合(t1 < 0)の判定を試してみます。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // 線分line0
        Vector2 p0{ 5,5 };
        Vector2 p1{ 15,11 };
        // 線分line1
        Vector2 p2{ 12,8 };
        Vector2 p3{ 15,6 };

        bool isCollision01 = MyMath::LineIntersection(p0, p1, p2, p3);

        mathGraph.DrawArrow(p0.x, p0.y, 0, 0, p1.x, p1.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line0
        mathGraph.DrawArrow(p2.x, p2.y, 0, 0, p3.x, p3.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line1

        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(p3.x, p3.y, 3, GetColor(0, 255, 255), TRUE);
        std::string p3_String = "p3=(" + std::to_string((int)p3.x) + "," + std::to_string((int)p3.y) + ")";
        mathGraph.DrawString(p3.x, p3.y, p3_String.c_str(), GetColor(0, 255, 255));


        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがですか？線line0と線line1が交差していていない(t1 < 0)ので線が白色で表示されましたか?
念のため、別の交差しない場合(1 < t1のとき)も試しておきましょう。

main.cppの点p1の位置を変更して線分line0と線分line1が交差しない場合(1 < t1)の判定を試してみます。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // 線分line0
        Vector2 p0{ 5,5 };
        Vector2 p1{ 15,11 };
        // 線分line1
        Vector2 p2{ 5,10 };
        Vector2 p3{ 9,9 };

        bool isCollision01 = MyMath::LineIntersection(p0, p1, p2, p3);

        mathGraph.DrawArrow(p0.x, p0.y, 0, 0, p1.x, p1.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line0
        mathGraph.DrawArrow(p2.x, p2.y, 0, 0, p3.x, p3.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line1

        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(p3.x, p3.y, 3, GetColor(0, 255, 255), TRUE);
        std::string p3_String = "p3=(" + std::to_string((int)p3.x) + "," + std::to_string((int)p3.y) + ")";
        mathGraph.DrawString(p3.x, p3.y, p3_String.c_str(), GetColor(0, 255, 255));


        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがですか？線line0と線line1が交差していていない(1 < t1)ので線が白色で表示されましたか?
これで、t1 < 0、1 < t1、t0 < 0、1 < t0 の4種類の交差しないパターンを試すことができました。
線と線の交差判定は、2Dゲームのレイ(光線)と壁や地面の直線との交差判定に使えますね。
ただし、その場合はレイ(光線)は有限の直線ではなくて片方に無限の直線なので、点p0をレイ(光線)の始点とするなら、
上記の「t0 < 1 の判定をあえてせずに」t0 が 1以上でもレイ(光線)があたっている、と判定する必要があります。
ではMyMathのLineIntersection関数を「t0 < 1 の判定をあえてしないように」改造してレイ(光線)の当たり判定を実現してみましょう。

MyMathクラスでレイ(光線)と線分(壁や床など)が交差するか判定する

MyMath.hを変更して光線ray0と線分line1が交差するかを求める関数RayLineCollision(判定のみ ver.)を追加してみましょう。

#ifndef MYMATH_H_
#define MYMATH_H_

#include "Vector2.h" // 線との当たり判定にVector2を使う

#include <cmath>

// 数学関連クラス
class MyMath
{
public:
   static const float Sqrt2; // = 1.41421356237f;　// √2

   static const float PI; // = 3.14159265359f; // 円周率
   static const float Deg2Rad; // = PI / 180f; // 度からラジアンに変換する定数

   (中略).....

    /// <summary>
    /// 光線ray0と線line1が重なっているかを調べる
    /// </summary>
    /// <param name="ray0start">光線ray0の始点</param>
    /// <param name="ray0dir">光線ray0の方向ベクトル</param>
    /// <param name="line1start">線line1の始点</param>
    /// <param name="line1end">線line1の終点</param>
    /// <returns>光線ray0と線line1が交差しているならtrue,してないならfalse</returns>
    static bool RayLineCollision(Vector2 ray0start, Vector2 ray0dir, Vector2 line1start, Vector2 line1end)
    {
        Vector2 v0 = ray0dir; // 光線ray0のベクトル
        Vector2 v1 = line1end - line1start; // line1の始点startから終点endへのベクトル
        Vector2 v01 = line1start - ray0start; // line0の始点からline1の始点へのベクトル 0start→1start
        float t1 = cross(v01, v0) / cross(v0, v1);
        float t0 = cross(v01, v1) / cross(v0, v1);

        // 光線ray0と線分line1が【交差しているか判定】
        if (0 < t1 && t1 < 1 && 0 < t0) return true; //【交差している】

        return false; // 光線ray0と線分line1は【交差していない】
    }

};

#endif

下図で上記コードの式との対応関係を確認してみてください。(v0をray0startに v1の代わりにray0dirに置き換えてみよう[オレンジの部分])

main.cppの点p0をray0posに、点p1の代わりにレイ光線の方向ray0dirに変更して、線分line1と交差するかの判定を試してみます。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // ray0光線レイ
        Vector2 ray0pos{ 5,5 }; // レイ光線の始点
        Vector2 ray0dir{ 1,1 }; // レイ光線の方向
        // 線分line1
        Vector2 p2{ 5,10 };
        Vector2 p3{ 15,6 };

        bool isCollision01 = MyMath::RayLineCollision(ray0pos, ray0dir, p2, p3);

        mathGraph.DrawArrow(ray0pos.x, ray0pos.y, 0, 0, ray0pos.x + ray0dir.x, ray0pos.y + ray0dir.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 光線ray0
        mathGraph.DrawArrow(p2.x, p2.y, 0, 0, p3.x, p3.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line1

        mathGraph.DrawPoint(ray0pos.x, ray0pos.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "ray0=(" + std::to_string((int)ray0pos.x) + "," + std::to_string((int)ray0pos.y) + ")";
        mathGraph.DrawString(ray0pos.x, ray0pos.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(p3.x, p3.y, 3, GetColor(0, 255, 255), TRUE);
        std::string p3_String = "p3=(" + std::to_string((int)p3.x) + "," + std::to_string((int)p3.y) + ")";
        mathGraph.DrawString(p3.x, p3.y, p3_String.c_str(), GetColor(0, 255, 255));


        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？レイの方向に有限の線分(壁や床)があるときに、線が赤色で表示されたでしょうか？
念のため、こんどはレイの方向を変えて、(-1,1) x方向に-1、y方向に+1の方向、
つまり、90°+45°=135°の方向のレイに変えた場合に光線と線分(壁や床)との当たり判定もためしてみましょう。

main.cppのレイ光線の方向ray0dirを(-1,1)=135°の方向に変更して、線分line1と交差するかの判定を試してみます。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // ray0光線レイ
        Vector2 ray0pos{ 5,5 }; // レイ光線の始点
        Vector2 ray0dir{ -1,1 }; // レイ光線の方向
        // 線分line1
        Vector2 p2{ 5,10 };
        Vector2 p3{ 15,6 };

        bool isCollision01 = MyMath::RayLineCollision(ray0pos, ray0dir, p2, p3);

        mathGraph.DrawArrow(ray0pos.x, ray0pos.y, 0, 0, ray0pos.x + ray0dir.x, ray0pos.y + ray0dir.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 光線ray0
        mathGraph.DrawArrow(p2.x, p2.y, 0, 0, p3.x, p3.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line1

        mathGraph.DrawPoint(ray0pos.x, ray0pos.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "ray0=(" + std::to_string((int)ray0pos.x) + "," + std::to_string((int)ray0pos.y) + ")";
        mathGraph.DrawString(ray0pos.x, ray0pos.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(p3.x, p3.y, 3, GetColor(0, 255, 255), TRUE);
        std::string p3_String = "p3=(" + std::to_string((int)p3.x) + "," + std::to_string((int)p3.y) + ")";
        mathGraph.DrawString(p3.x, p3.y, p3_String.c_str(), GetColor(0, 255, 255));


        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }



        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？こんどはレイ光線の方向に線分(壁や床)がないので線が白色で表示されましたでしょうか？

このように、数学の式の理解をすると、数式を少しだけ変えて(1 < t0) t0 の1以上の判定をしないだけで、
ゲームに実際に使えるようなレイの判定をできることが実感できたでしょうか?

Unityに最初から用意されている機能に頼ってしまうと、このようなゲームを支える数学の基礎を学ぶ機会のないまま、就職活動をすることになってしまいます。
すると、「Unityだけ」でゲームを作っている人は「ベクトルとか当たり判定の基礎の知識が薄い」のではないかとベテランのプログラマからは見られているわけです。
2010年代以降の「Unity以降」世代と2010年以前の「自力勉強世代」との間の「ゲーム数学の勉強する機会格差」が生じてしまっています。
結果として、「自作ゲームは作れる」のに「ゲームプログラマ」としては就職に苦労する「世代ギャップ」が生じています。
「Unity」などのゲームエンジンの便利さにより、ゲームプログラマの「基礎的な数学力」の足腰とモチベーションをぐらつかせているという意味で、
Unityの教育の手軽さに対する「反作用」がでてきているともいえます。
(最近だと、デザイナー系や美大の学科なんかも自力でUnity勉強して、かっこいいゲーム作ってきちゃうので、差別化が大変なのです)
デザイナー系や美大の学科が、絶対に勉強してこない(勉強したくない)ような分野の代表が「ベクトルや当たり判定」なのです。

MyMathクラスでレイ(光線)と線分(壁や床など)の交点を求める

MyMath.hを変更して光線ray0と線分line1の交点を求める関数RayLineCollision(交点も求める ver.)を変更してみましょう。

#ifndef MYMATH_H_
#define MYMATH_H_

#include "Vector2.h" // 線との当たり判定にVector2を使う

#include <cmath>

// 数学関連クラス
class MyMath
{
public:
   static const float Sqrt2; // = 1.41421356237f;　// √2

   static const float PI; // = 3.14159265359f; // 円周率
   static const float Deg2Rad; // = PI / 180f; // 度からラジアンに変換する定数

   (中略).....

    /// <summary>
    /// 光線ray0と線line1が重なっているかを調べる
    /// </summary>
    /// <param name="result"光線ray0と線line1の交点を求めてresultで返す</param>
    /// <param name="ray0start">光線ray0の始点</param>
    /// <param name="ray0dir">光線ray0の方向ベクトル</param>
    /// <param name="line1start">線line1の始点</param>
    /// <param name="line1end">線line1の終点</param>
    /// <returns>光線ray0と線line1が交差しているならtrue,してないならfalse</returns>
    static bool RayLineCollision(Vector2& result, Vector2 ray0start, Vector2 ray0dir, Vector2 line1start, Vector2 line1end)
    {
        Vector2 v0 = ray0dir; // 光線ray0のベクトル
        Vector2 v1 = line1end - line1start; // line1の始点startから終点endへのベクトル
        Vector2 v01 = line1start - ray0start; // line0の始点からline1の始点へのベクトル 0start→1start
        float t1 = cross(v01, v0) / cross(v0, v1);
        float t0 = cross(v01, v1) / cross(v0, v1);

        result = ray0start + v0 * t0; //交点resultを求めて【&result参照で返却】

        // 光線ray0と線分line1が【交差しているか判定】
        if (0 < t1 && t1 < 1 && 0 < t0) return true; //【交差している】

        return false; // 光線ray0と線分line1は【交差していない】
    }

};

#endif

下図で上記コードの式との対応関係を確認してみてください。

main.cppに交点Qを追加して関数の引数に渡して、線分line1と光線ray0の交点を求めて表示してみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // ray0光線レイ
        Vector2 ray0pos{ 5,5 }; // レイ光線の始点
        Vector2 ray0dir{ -1,1 }; // レイ光線の方向
        // 線分line1
        Vector2 p2{ 5,10 };
        Vector2 p3{ 15,6 };

        Vector2 Q; // 光線ray0とline1の交点
        bool isCollision01 = MyMath::RayLineCollision(Q, ray0pos, ray0dir, p2, p3);

        mathGraph.DrawArrow(ray0pos.x, ray0pos.y, 0, 0, ray0pos.x + ray0dir.x, ray0pos.y + ray0dir.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 光線ray0
        mathGraph.DrawArrow(p2.x, p2.y, 0, 0, p3.x, p3.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line1

        mathGraph.DrawPoint(ray0pos.x, ray0pos.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "ray0=(" + std::to_string((int)ray0pos.x) + "," + std::to_string((int)ray0pos.y) + ")";
        mathGraph.DrawString(ray0pos.x, ray0pos.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(p3.x, p3.y, 3, GetColor(0, 255, 255), TRUE);
        std::string p3_String = "p3=(" + std::to_string((int)p3.x) + "," + std::to_string((int)p3.y) + ")";
        mathGraph.DrawString(p3.x, p3.y, p3_String.c_str(), GetColor(0, 255, 255));

        mathGraph.DrawPoint(Q.x, Q.y, 3, GetColor(255, 165, 0), TRUE);
        std::string Q_String = "Q=(" + std::to_string(Q.x) + "," + std::to_string(Q.y) + ")";
        mathGraph.DrawString(Q.x, Q.y - 10, Q_String.c_str(), GetColor(255, 165, 0));


        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？なるほど、レイ光線の方向に線分(壁や床)がないときは、線分line1の延長線上に交点Qが求まるのですね。
では、光線の方向が壁と逆方向(-1,-1)の場合はどうなるか実験してみましょう。

main.cppの交点Qが光線ray0と逆方向(-1,-1)の場合の交点を表示してみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // ray0光線レイ
        Vector2 ray0pos{ 5,5 }; // レイ光線の始点
        Vector2 ray0dir{ -1,-1 }; // レイ光線の方向
        // 線分line1
        Vector2 p2{ 5,10 };
        Vector2 p3{ 15,6 };

        Vector2 Q; // 光線ray0とline1の交点
        bool isCollision01 = MyMath::RayLineCollision(Q, ray0pos, ray0dir, p2, p3);

        mathGraph.DrawArrow(ray0pos.x, ray0pos.y, 0, 0, ray0pos.x + ray0dir.x, ray0pos.y + ray0dir.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 光線ray0
        mathGraph.DrawArrow(p2.x, p2.y, 0, 0, p3.x, p3.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line1

        mathGraph.DrawPoint(ray0pos.x, ray0pos.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "ray0=(" + std::to_string((int)ray0pos.x) + "," + std::to_string((int)ray0pos.y) + ")";
        mathGraph.DrawString(ray0pos.x, ray0pos.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(p3.x, p3.y, 3, GetColor(0, 255, 255), TRUE);
        std::string p3_String = "p3=(" + std::to_string((int)p3.x) + "," + std::to_string((int)p3.y) + ")";
        mathGraph.DrawString(p3.x, p3.y, p3_String.c_str(), GetColor(0, 255, 255));

        mathGraph.DrawPoint(Q.x, Q.y, 3, GetColor(255, 165, 0), TRUE);
        std::string Q_String = "Q=(" + std::to_string(Q.x) + "," + std::to_string(Q.y) + ")";
        mathGraph.DrawString(Q.x, Q.y - 10, Q_String.c_str(), GetColor(255, 165, 0));


        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？なるほど、逆方向の場合はレイ光線の後ろ側に交点が数学的に求まって、表示されるのですね。
では、今度こそレイ光線が壁(線分)にヒットするときの実験をしてみましょう。

main.cppを変更して、光線ray0の方向が(1,1)で壁(線)とぶつかる場合にその交点Qを表示してみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // ray0光線レイ
        Vector2 ray0pos{ 5,5 }; // レイ光線の始点
        Vector2 ray0dir{ 1,1 }; // レイ光線の方向
        // 線分line1
        Vector2 p2{ 5,10 };
        Vector2 p3{ 15,6 };

        Vector2 Q; // 光線ray0とline1の交点
        bool isCollision01 = MyMath::RayLineCollision(Q, ray0pos, ray0dir, p2, p3);

        mathGraph.DrawArrow(ray0pos.x, ray0pos.y, 0, 0, ray0pos.x + ray0dir.x, ray0pos.y + ray0dir.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 光線ray0
        mathGraph.DrawArrow(p2.x, p2.y, 0, 0, p3.x, p3.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line1

        mathGraph.DrawPoint(ray0pos.x, ray0pos.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "ray0=(" + std::to_string((int)ray0pos.x) + "," + std::to_string((int)ray0pos.y) + ")";
        mathGraph.DrawString(ray0pos.x, ray0pos.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(p3.x, p3.y, 3, GetColor(0, 255, 255), TRUE);
        std::string p3_String = "p3=(" + std::to_string((int)p3.x) + "," + std::to_string((int)p3.y) + ")";
        mathGraph.DrawString(p3.x, p3.y, p3_String.c_str(), GetColor(0, 255, 255));

        mathGraph.DrawPoint(Q.x, Q.y, 3, GetColor(255, 165, 0), TRUE);
        std::string Q_String = "Q=(" + std::to_string(Q.x) + "," + std::to_string(Q.y) + ")";
        mathGraph.DrawString(Q.x, Q.y - 10, Q_String.c_str(), GetColor(255, 165, 0));


        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？つまり、この設計した関数を使う場合は、isCollision01でMyMath::RayLineCollisionの結果をbool型で受けて、
レイ光線がぶつかったかどうかと、セットで交点Qを使う必要があるのですね。
逆に言えば、isCollision01を無視すれば、壁や床が無限の長さのときの交点を求めるのにも、この関数は応用できるということですね。

MyMathクラスで線と線の交点を求める

MyMath.hを変更して線分line0と線分line1の交点を関数LineIntersection(交点も求める ver.)で求められるようにしてみましょう。

#ifndef MYMATH_H_
#define MYMATH_H_

#include "Vector2.h" // 線との当たり判定にVector2を使う

#include <cmath>

// 数学関連クラス
class MyMath
{
public:
   static const float Sqrt2; // = 1.41421356237f;　// √2

   static const float PI; // = 3.14159265359f; // 円周率
   static const float Deg2Rad; // = PI / 180f; // 度からラジアンに変換する定数

   (中略).....

    /// <summary>
    /// 線line0と線line1が重なっているかを調べる
    /// </summary>
    /// <param name="result">線line0と線line1の交点を求めてresultで返す</param>
    /// <param name="line0start">線line0の始点</param>
    /// <param name="line0end">線line0の終点</param>
    /// <param name="line1start">線line1の始点</param>
    /// <param name="line1end">線line1の終点</param>
    /// <returns>線line0と線line1が交差しているならtrue,してないならfalse</returns>
    static bool LineIntersection(Vector2& result, Vector2 line0start, Vector2 line0end, Vector2 line1start, Vector2 line1end)
    {
        Vector2 v0 = line0end - line0start; // line0の始点startから終点endへのベクトル
        Vector2 v1 = line1end - line1start; // line1の始点startから終点endへのベクトル
        Vector2 v01 = line1start - line0start; // line0の始点からline1の始点へのベクトル 0start→1start
        float t1 = cross(v01, v0) / cross(v0, v1);
        float t0 = cross(v01, v1) / cross(v0, v1);

        result = line0start + v0 * t0; //交点resultを求めて【&result参照で返却】

        // 線分line0と線分line1が【交差しているか判定】
        if (0 < t1 && t1 < 1 && 0 < t0 && t0 < 1) return true; //【交差している】

        return false; // 線分line0と線分line1は【交差していない】
    }

};

#endif

下図で上記コードの式との対応関係を確認してみてください。

main.cppを変更して、線分line0と線分line1の交点を求めて表示してみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // line0
        Vector2 p0{ 5,5 }; // line0の始点
        Vector2 p1{ 15,11 }; // line0の終点
        // 線分line1
        Vector2 p2{ 5,10 };
        Vector2 p3{ 15,6 };

        Vector2 Q; // line0とline1の交点
        bool isCollision01 = MyMath::LineIntersection(Q, p0, p1, p2, p3);

        mathGraph.DrawArrow(p0.x, p0.y, 0, 0, p1.x, p1.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line0
        mathGraph.DrawArrow(p2.x, p2.y, 0, 0, p3.x, p3.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line1

        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(p3.x, p3.y, 3, GetColor(0, 255, 255), TRUE);
        std::string p3_String = "p3=(" + std::to_string((int)p3.x) + "," + std::to_string((int)p3.y) + ")";
        mathGraph.DrawString(p3.x, p3.y, p3_String.c_str(), GetColor(0, 255, 255));

        mathGraph.DrawPoint(Q.x, Q.y, 3, GetColor(255, 165, 0), TRUE);
        std::string Q_String = "Q=(" + std::to_string(Q.x) + "," + std::to_string(Q.y) + ")";
        mathGraph.DrawString(Q.x, Q.y - 10, Q_String.c_str(), GetColor(255, 165, 0));


        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？線分line0と線分line1の交点Qが表示されましたか?
レイキャストと線分どうしの交差判定は基礎となっている数式は共通だという実感が湧いたでしょうか。
つまり、2Dのレイキャストは裏側で外積crossを使って、高速に計算されているのです。

MyMathクラスで壁(線)に対する点の反射(線の終点の反射位置と交点)を求める

MyMath.hを変更して線(壁)wall0と線分line1の交点とline1の反射点を関数LineReflectionで求められるようにしてみましょう。

#ifndef MYMATH_H_
#define MYMATH_H_

#include "Vector2.h" // 線との当たり判定にVector2を使う

#include <cmath>

// 数学関連クラス
class MyMath
{
public:
   static const float Sqrt2; // = 1.41421356237f;　// √2

   static const float PI; // = 3.14159265359f; // 円周率
   static const float Deg2Rad; // = PI / 180f; // 度からラジアンに変換する定数

   (中略).....

    /// <summary>
    /// 壁wall0(start→end)に対する線line1(start→end)の反射位置を求める
    /// </summary>
    /// <param name="reflectPoint">壁から反射したポイント点がreturnされる</param>
    /// <param name="collisionPoint">壁に衝突したポイント点がreturnされる</param>
    /// <param name="wall0start">壁の起点wall0start</param>
    /// <param name="wall0end">壁の終点wall0end</param>
    /// <param name="line1start">線bの起点line1start</param>
    /// <param name="line1end">線bの終点line1end</param>
    /// <returns>線line0(start→end)が壁wall0に接触するか?</returns>
    static bool LineReflection(Vector2& reflectPoint, Vector2& collisionPoint,
        Vector2 wall0start, Vector2 wall0end, Vector2 line1start, Vector2 line1end)
    {
        Vector2 wall0 = wall0end - wall0start;
        Vector2 line1 = line1end - line1start;
        Vector2 e0 = wall0.normalized(); // 壁(wall0start→wall0end)の単位ベクトル
        Vector2 v01 = line1end - wall0start;
        float cross_e0_v01 = cross(e0, v01);
        float L = std::abs(cross_e0_v01); // |外積| (外積の絶対値をabsで求める)
        Vector2 n; // 壁の法線ベクトル
        if(cross_e0_v01 < 0) // 外積がプラスかマイナスかで壁のサイドが変わるので法線ベクトルnの方向切替
            n = Vector2(-wall0.y, wall0.x).normalized(); // 法線ベクトル (-y,x)の単位ベクトル
        else
            n = Vector2(wall0.y, -wall0.x).normalized(); // 法線ベクトル (y,-x)の単位ベクトル

        // 壁wall0と線分line1が交差しているか調べ、その交点をcollisionPointに得る
        bool isCollision = LineIntersection(collisionPoint, wall0start, wall0end, line1start, line1end);

        reflectPoint = line1end + 2 * L * n; // 壁wall0(start→end)に対する線line1(start→end)の終点line1endの反射点

        return isCollision; // 壁wall0と線分line1が交差するかをreturnする
    }

};

#endif

壁wall0と線line1が交差しているか？とその交点を求める処理は、先に作ってあった線と線の交差LineIntersectionを再利用しています。
なので、反射のキーとなる式は 「反射点 = line1の終点 + 2 × L × 法線n 」ですね。この式は3Dの反射でも使われている式です。
下図で上記コードの式との対応関係を確認してみてください。

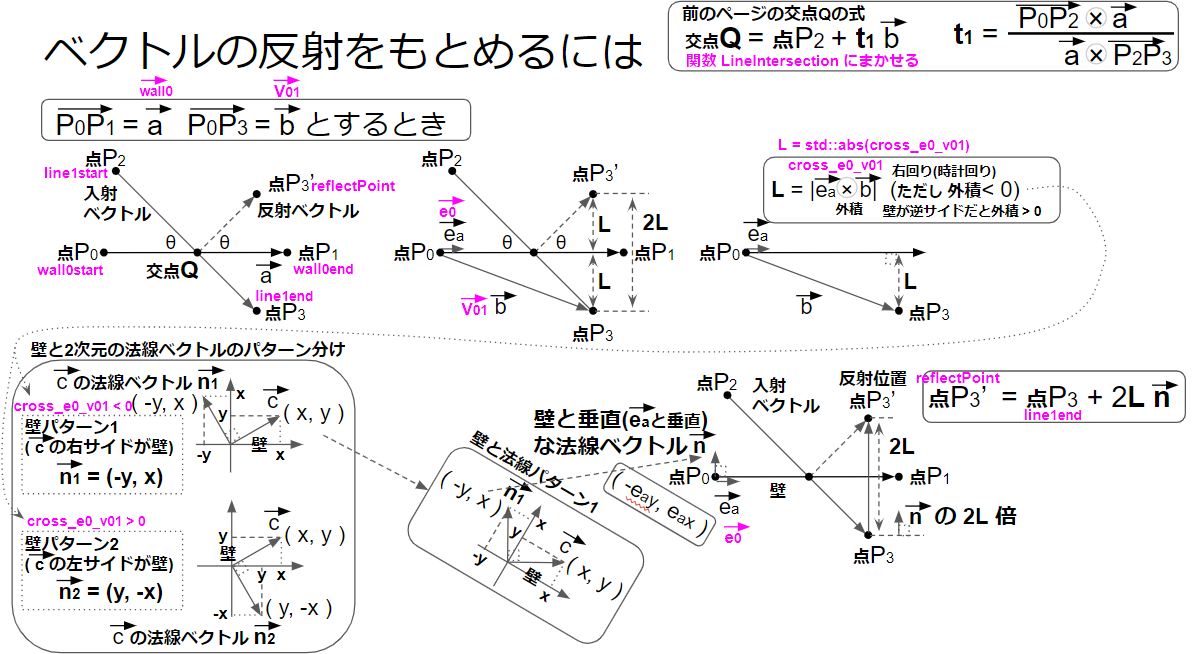
main.cppを変更して、壁(線)line0 に対する線分line1の交点Q と line1の終点p3の反射点R を求めて表示してみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // line0
        Vector2 p0{ 5,5 }; // line0の始点
        Vector2 p1{ 15,11 }; // line0の終点
        // 線分line1
        Vector2 p2{ 5,10 };
        Vector2 p3{ 15,6 };

        Vector2 Q; // line0とline1の交点
        Vector2 R; // line0を壁wall0とした場合のline1の終点p3の壁line0に対する反射点Rと交点Qを求める
        bool isCollision01 = MyMath::LineReflection(R, Q, p0, p1, p2, p3);

        mathGraph.DrawArrow(p0.x, p0.y, 0, 0, p1.x, p1.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line0
        mathGraph.DrawArrow(p2.x, p2.y, 0, 0, p3.x, p3.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line1

        // 反射ベクトル(交点Q→反射点R)を描く
        if (isCollision01)
            mathGraph.DrawArrow(Q.x, Q.y, 0, 0, R.x, R.y, 0.8f, 1.0f, GetColor(255, 255, 0));

        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(p3.x, p3.y, 3, GetColor(0, 255, 255), TRUE);
        std::string p3_String = "p3=(" + std::to_string((int)p3.x) + "," + std::to_string((int)p3.y) + ")";
        mathGraph.DrawString(p3.x, p3.y, p3_String.c_str(), GetColor(0, 255, 255));

        mathGraph.DrawPoint(Q.x, Q.y, 3, GetColor(255, 165, 0), TRUE);
        std::string Q_String = "Q=(" + std::to_string(Q.x) + "," + std::to_string(Q.y) + ")";
        mathGraph.DrawString(Q.x, Q.y - 10, Q_String.c_str(), GetColor(255, 165, 0));

        mathGraph.DrawPoint(R.x, R.y, 3, GetColor(255, 255, 0), TRUE);
        std::string R_String = "R=(" + std::to_string(R.x) + "," + std::to_string(R.y) + ")";
        mathGraph.DrawString(R.x, R.y - 10, R_String.c_str(), GetColor(255, 255, 0));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？壁(線)line0(wall0) に対する線分line1の終点p3 の反射点R と交点Q が表示されましたか?
交点Qは先に作っておいた線と線の交点を求める関数LineIntersectionが再利用されています。
念のため、壁と線が交差しないときはどうなるかも実験しておきましょう。

main.cppを変更して、壁(線)line0 と線分line1が交差しない場合(t0 < 0)を実験で表示してみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // line0
        Vector2 p0{ 11,9 }; // line0の始点
        Vector2 p1{ 15,11 }; // line0の終点
        // 線分line1
        Vector2 p2{ 5,10 };
        Vector2 p3{ 15,6 };

        Vector2 Q; // line0とline1の交点
        Vector2 R; // line0を壁wall0とした場合のline1の終点p3の壁line0に対する反射点Rと交点Qを求める
        bool isCollision01 = MyMath::LineReflection(R, Q, p0, p1, p2, p3);

        mathGraph.DrawArrow(p0.x, p0.y, 0, 0, p1.x, p1.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line0
        mathGraph.DrawArrow(p2.x, p2.y, 0, 0, p3.x, p3.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line1

        // 反射ベクトル(交点Q→反射点R)を描く
        if (isCollision01)
            mathGraph.DrawArrow(Q.x, Q.y, 0, 0, R.x, R.y, 0.8f, 1.0f, GetColor(255, 255, 0));

        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(p3.x, p3.y, 3, GetColor(0, 255, 255), TRUE);
        std::string p3_String = "p3=(" + std::to_string((int)p3.x) + "," + std::to_string((int)p3.y) + ")";
        mathGraph.DrawString(p3.x, p3.y, p3_String.c_str(), GetColor(0, 255, 255));

        mathGraph.DrawPoint(Q.x, Q.y, 3, GetColor(255, 165, 0), TRUE);
        std::string Q_String = "Q=(" + std::to_string(Q.x) + "," + std::to_string(Q.y) + ")";
        mathGraph.DrawString(Q.x, Q.y - 10, Q_String.c_str(), GetColor(255, 165, 0));

        mathGraph.DrawPoint(R.x, R.y, 3, GetColor(255, 255, 0), TRUE);
        std::string R_String = "R=(" + std::to_string(R.x) + "," + std::to_string(R.y) + ")";
        mathGraph.DrawString(R.x, R.y - 10, R_String.c_str(), GetColor(255, 255, 0));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？あーなるほど、壁(線)line0(wall0)が途切れている場合でも、「その延長線上に交点Qは求まり」反射点R は「その交点Qに対する反射」として計算はされるんですね。
ということは、壁の長さがwall0startと逆方向に無限な場合は、(t0 < 0)のときの当たり判定を許して、反射点を調べれば求められそうですね。
では、こんどは(1 < t0)の場合も実験してみましょう。

main.cppを変更して、壁(線)line0 と線分line1が交差しない場合(1 < t0)を実験で表示してみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // line0
        Vector2 p0{ 5,5 }; // line0の始点
        Vector2 p1{ 9,7 }; // line0の終点
        // 線分line1
        Vector2 p2{ 5,10 };
        Vector2 p3{ 15,6 };

        Vector2 Q; // line0とline1の交点
        Vector2 R; // line0を壁wall0とした場合のline1の終点p3の壁line0に対する反射点Rと交点Qを求める
        bool isCollision01 = MyMath::LineReflection(R, Q, p0, p1, p2, p3);

        mathGraph.DrawArrow(p0.x, p0.y, 0, 0, p1.x, p1.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line0
        mathGraph.DrawArrow(p2.x, p2.y, 0, 0, p3.x, p3.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line1

        // 反射ベクトル(交点Q→反射点R)を描く
        if (isCollision01)
            mathGraph.DrawArrow(Q.x, Q.y, 0, 0, R.x, R.y, 0.8f, 1.0f, GetColor(255, 255, 0));

        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(p3.x, p3.y, 3, GetColor(0, 255, 255), TRUE);
        std::string p3_String = "p3=(" + std::to_string((int)p3.x) + "," + std::to_string((int)p3.y) + ")";
        mathGraph.DrawString(p3.x, p3.y, p3_String.c_str(), GetColor(0, 255, 255));

        mathGraph.DrawPoint(Q.x, Q.y, 3, GetColor(255, 165, 0), TRUE);
        std::string Q_String = "Q=(" + std::to_string(Q.x) + "," + std::to_string(Q.y) + ")";
        mathGraph.DrawString(Q.x, Q.y - 10, Q_String.c_str(), GetColor(255, 165, 0));

        mathGraph.DrawPoint(R.x, R.y, 3, GetColor(255, 255, 0), TRUE);
        std::string R_String = "R=(" + std::to_string(R.x) + "," + std::to_string(R.y) + ")";
        mathGraph.DrawString(R.x, R.y - 10, R_String.c_str(), GetColor(255, 255, 0));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？はい、なるほど予感通り、壁(線)line0(wall0)が「終点end側(点p1)で」途切れている場合でも「その延長線上に交点Qは求まり」反射点R は「その交点Qに対する反射」として計算されました。
ということは、壁の長さがwall0endから先の方向に無限な場合は、(1 < t0)のときの当たり判定を許して、反射点を調べれば求められそうですね。
では、こんどは(t1 < 0)の場合も実験してみましょう。

main.cppを変更して、壁(線)line0 と線分line1が交差しない場合(t1 < 0)を実験で表示してみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // line0
        Vector2 p0{ 5,5 }; // line0の始点
        Vector2 p1{ 15,11 }; // line0の終点
        // 線分line1
        Vector2 p2{ 12,8 };
        Vector2 p3{ 15,6 };

        Vector2 Q; // line0とline1の交点
        Vector2 R; // line0を壁wall0とした場合のline1の終点p3の壁line0に対する反射点Rと交点Qを求める
        bool isCollision01 = MyMath::LineReflection(R, Q, p0, p1, p2, p3);

        mathGraph.DrawArrow(p0.x, p0.y, 0, 0, p1.x, p1.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line0
        mathGraph.DrawArrow(p2.x, p2.y, 0, 0, p3.x, p3.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line1

        // 反射ベクトル(交点Q→反射点R)を描く
        if (isCollision01)
            mathGraph.DrawArrow(Q.x, Q.y, 0, 0, R.x, R.y, 0.8f, 1.0f, GetColor(255, 255, 0));

        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(p3.x, p3.y, 3, GetColor(0, 255, 255), TRUE);
        std::string p3_String = "p3=(" + std::to_string((int)p3.x) + "," + std::to_string((int)p3.y) + ")";
        mathGraph.DrawString(p3.x, p3.y, p3_String.c_str(), GetColor(0, 255, 255));

        mathGraph.DrawPoint(Q.x, Q.y, 3, GetColor(255, 165, 0), TRUE);
        std::string Q_String = "Q=(" + std::to_string(Q.x) + "," + std::to_string(Q.y) + ")";
        mathGraph.DrawString(Q.x, Q.y - 10, Q_String.c_str(), GetColor(255, 165, 0));

        mathGraph.DrawPoint(R.x, R.y, 3, GetColor(255, 255, 0), TRUE);
        std::string R_String = "R=(" + std::to_string(R.x) + "," + std::to_string(R.y) + ")";
        mathGraph.DrawString(R.x, R.y - 10, R_String.c_str(), GetColor(255, 255, 0));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？うーん、こんどはline1の飛んでいく方向が壁と逆の場合でも「飛んでいく方向と逆方向に交点Qは求まり」反射点R は「壁を鏡にした飛んでいく位置」として計算されました。
うーむ鏡の国のボール(青)の飛んでいくベクトルが、(t1 < 0)のときの当たり判定を許して、反射点を調べれば求められるようなイメージでしょうか。
では、こんどは(1 < t1)の場合も実験してみましょう。

main.cppを変更して、壁(線)line0 と線分line1が交差しない場合(1 < t1)を実験で表示してみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // line0
        Vector2 p0{ 5,5 }; // line0の始点
        Vector2 p1{ 15,11 }; // line0の終点
        // 線分line1
        Vector2 p2{ 5,10 };
        Vector2 p3{ 9,9 };

        Vector2 Q; // line0とline1の交点
        Vector2 R; // line0を壁wall0とした場合のline1の終点p3の壁line0に対する反射点Rと交点Qを求める
        bool isCollision01 = MyMath::LineReflection(R, Q, p0, p1, p2, p3);

        mathGraph.DrawArrow(p0.x, p0.y, 0, 0, p1.x, p1.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line0
        mathGraph.DrawArrow(p2.x, p2.y, 0, 0, p3.x, p3.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line1

        // 反射ベクトル(交点Q→反射点R)を描く
        if (isCollision01)
            mathGraph.DrawArrow(Q.x, Q.y, 0, 0, R.x, R.y, 0.8f, 1.0f, GetColor(255, 255, 0));

        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(p3.x, p3.y, 3, GetColor(0, 255, 255), TRUE);
        std::string p3_String = "p3=(" + std::to_string((int)p3.x) + "," + std::to_string((int)p3.y) + ")";
        mathGraph.DrawString(p3.x, p3.y, p3_String.c_str(), GetColor(0, 255, 255));

        mathGraph.DrawPoint(Q.x, Q.y, 3, GetColor(255, 165, 0), TRUE);
        std::string Q_String = "Q=(" + std::to_string(Q.x) + "," + std::to_string(Q.y) + ")";
        mathGraph.DrawString(Q.x, Q.y - 10, Q_String.c_str(), GetColor(255, 165, 0));

        mathGraph.DrawPoint(R.x, R.y, 3, GetColor(255, 255, 0), TRUE);
        std::string R_String = "R=(" + std::to_string(R.x) + "," + std::to_string(R.y) + ")";
        mathGraph.DrawString(R.x, R.y - 10, R_String.c_str(), GetColor(255, 255, 0));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？うーん、なるほど、line1の「始点p2の青のボールが壁に当たらない場合も交点Qは求まり」反射点R は「壁を鏡にした移動後のボール(緑)の鏡に映った位置(黄)」でしょうか。
うーむ鏡に映った線分line0の鏡像が、(1 < t1)のときの当たり判定を許して、反射点を調べれば求められるようなイメージでしょうか(うーん使いどころがあるかは謎)。
t0、t1について実験をすると、反射点はなかなか奥が深いですね。
実際に反射を求めるときには、衝突するかのisCollision01とセットで使うのが必須ですね。そうしないと反射していないときに壁の向こう側にボールがめり込んじゃいますからね。

MyMathクラスで壁(線)に対する円(半径r)の反射(円の中心点の反射位置と円の反射する瞬間の中心点)を求める

MyMath.hを変更して線(壁)wall0と線分line1の交点とline1endを中心とする半径rの円の反射点を関数LineReflectionで求められるようにしてみましょう。

#ifndef MYMATH_H_
#define MYMATH_H_

#include "Vector2.h" // 線との当たり判定にVector2を使う

#include <cmath>

// 数学関連クラス
class MyMath
{
public:
   static const float Sqrt2; // = 1.41421356237f;　// √2

   static const float PI; // = 3.14159265359f; // 円周率
   static const float Deg2Rad; // = PI / 180f; // 度からラジアンに変換する定数

   (中略).....

    /// <summary>
    /// 壁wall0(start→end)に対する線line1(start→end)の反射位置を求める
    /// </summary>
    /// <param name="reflectPoint">壁から反射したポイント点がreturnされる</param>
    /// <param name="collisionPoint">壁に衝突したポイント点がreturnされる</param>
    /// <param name="wall0start">壁の起点wall0start</param>
    /// <param name="wall0end">壁の終点wall0end</param>
    /// <param name="line1start">線bの起点line1start</param>
    /// <param name="line1end">線bの終点line1end</param>
    /// <param name="r">点line1startが点じゃなく円の場合はr=円の半径とするr=0なら点扱い</param>
    /// <returns>線line0(start→end)が壁wall0に接触するか?</returns>
    static bool LineReflection(Vector2& reflectPoint, Vector2& collisionPoint,
        Vector2 wall0start, Vector2 wall0end, Vector2 line1start, Vector2 line1end, float r = 0)
    {
        Vector2 wall0 = wall0end - wall0start;
        Vector2 line1 = line1end - line1start;
        Vector2 e0 = wall0.normalized(); // 壁(wall0start→wall0end)の単位ベクトル
        Vector2 v01 = line1end - wall0start;
        float cross_e0_v01 = cross(e0, v01);
        float L = r + std::abs(cross_e0_v01); // |外積| (外積の絶対値をabsで求める)
        Vector2 n; // 壁の法線ベクトル
        if(cross_e0_v01 < 0) // 外積がプラスかマイナスかで壁のサイドが変わるので法線ベクトルnの方向切替
            n = Vector2(-wall0.y, wall0.x).normalized(); // 法線ベクトル (-y,x)の単位ベクトル
        else
            n = Vector2(wall0.y, -wall0.x).normalized(); // 法線ベクトル (y,-x)の単位ベクトル

        // 壁wall0と線分line1が交差しているか調べ、その交点をcollisionPointに得る
        bool isCollision = LineIntersection(collisionPoint, wall0start, wall0end, line1start, line1end);

        if(r > 0) // 半径が0以上のときは球の場合として衝突点を求めなおす
        {   // 点(r==0)じゃなくて半径rが0じゃない円の反射計算のときだけ円の衝突点を計算
            float dot_line1_n = dot(line1, n); // 内積 line1・n
            float t = L / dot_line1_n;
            collisionPoint = line1end + line1 * t; // 円の場合の衝突点を求める
        }

        reflectPoint = line1end + 2 * L * n; // 壁wall0(start→end)に対する線line1(start→end)の終点line1endの反射点

        return isCollision; // 壁wall0と線分line1が交差するかをreturnする
    }

};

#endif

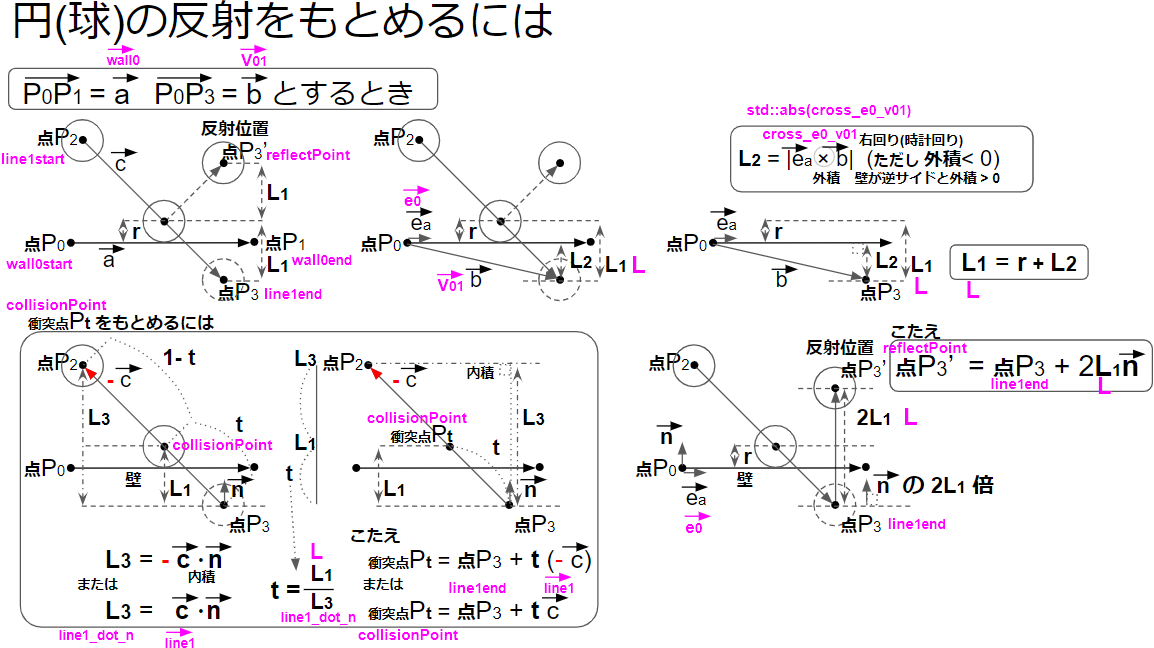
下図で上記コードの式との対応関係を確認してみてください。半径rが0じゃないときに衝突点Pt(collisionPoint)をline1と法線nの内積を使って求めなおしています。
注意点として、isCollisionは線と線の交差するかの判定を使っているので、厳密にはline0の始点P0と終点P1付近で線としては交差してないけど円と点が触れているときの判定はバグっちゃいそうですね。

main.cppを変更して、壁(線)line0 に対する線分line1方向に進む円(半径r)の衝突した瞬間の円の中心Q と反射した円の中心点R を求めて表示してみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // line0
        Vector2 p0{ 5,5 }; // line0の始点
        Vector2 p1{ 15,11 }; // line0の終点
        // 線分line1
        Vector2 p2{ 5,10 };
        Vector2 p3{ 15,6 };
        float r = 1.0f; // 円の半径r 始点p2が円(青ボール)の場合を想定

        Vector2 Q; // line0とline1の交点
        Vector2 R; // line0を壁wall0とした場合のline1の終点p3の壁line0に対する反射点Rと交点Qを求める
        bool isCollision01 = MyMath::LineReflection(R, Q, p0, p1, p2, p3, r);

        mathGraph.DrawCircle(p2.x, p2.y, r, GetColor(0, 0, 255), FALSE); // 円p2(始点)を描く
        mathGraph.DrawCircle(Q.x, Q.y, r, GetColor(255, 165, 0), FALSE); // 円Q(衝突位置)を描く
        mathGraph.DrawCircle(R.x, R.y, r, GetColor(255, 255, 0), FALSE); // 円R(反射位置)を描く

        mathGraph.DrawArrow(p0.x, p0.y, 0, 0, p1.x, p1.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line0
        mathGraph.DrawArrow(p2.x, p2.y, 0, 0, p3.x, p3.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line1

        // 反射ベクトル(交点Q→反射点R)を描く
        if (isCollision01)
            mathGraph.DrawArrow(Q.x, Q.y, 0, 0, R.x, R.y, 0.8f, 1.0f, GetColor(255, 255, 0));

        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(p3.x, p3.y, 3, GetColor(0, 255, 255), TRUE);
        std::string p3_String = "p3=(" + std::to_string((int)p3.x) + "," + std::to_string((int)p3.y) + ")";
        mathGraph.DrawString(p3.x, p3.y, p3_String.c_str(), GetColor(0, 255, 255));

        mathGraph.DrawPoint(Q.x, Q.y, 3, GetColor(255, 165, 0), TRUE);
        std::string Q_String = "Q=(" + std::to_string(Q.x) + "," + std::to_string(Q.y) + ")";
        mathGraph.DrawString(Q.x, Q.y - 10, Q_String.c_str(), GetColor(255, 165, 0));

        mathGraph.DrawPoint(R.x, R.y, 3, GetColor(255, 255, 0), TRUE);
        std::string R_String = "R=(" + std::to_string(R.x) + "," + std::to_string(R.y) + ")";
        mathGraph.DrawString(R.x, R.y - 10, R_String.c_str(), GetColor(255, 255, 0));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？青ボール(始点p2)が壁(線)line0(wall0) に反射(衝突点Q:だいだい色ボール)して反射点R(黄色ボール)に飛んでいく様子が表示されましたか?
厳密には、isCollision01は線と線の交点を求める関数LineIntersectionが再利用されているため、壁始点p0 と壁終点p1 付近で判定がバグります。
壁始点p0と壁終点p1の判定は別途考える必要があります。

MyMathクラスでレイ光線と円(半径r)の当たり判定と交点を求める

MyMath.hを変更してレイ光線ray0と円(中心点:pc 半径:r)の当たり判定と交点を関数RayCircleCollisionで求められるようにしてみましょう。

#ifndef MYMATH_H_
#define MYMATH_H_

#include "Vector2.h" // 線との当たり判定にVector2を使う

#include <cmath>

// 数学関連クラス
class MyMath
{
public:
   static const float Sqrt2; // = 1.41421356237f;　// √2

   static const float PI; // = 3.14159265359f; // 円周率
   static const float Deg2Rad; // = PI / 180f; // 度からラジアンに変換する定数

   (中略).....

    /// <summary>
    /// 光線ray0と円(中心:pc 半径:r)が重なっているかを調べる
    /// </summary>
    /// <param name="result1">光線ray0と円の交点1(最初に交わる点)</param>
    /// <param name="result2">光線ray0と円の交点2(後ろ側で交わる点)</param>
    /// <param name="result_isInsideCircle">レイの始点が円の内側にあるかの結果がtrueかfalseで求まる</param>
    /// <param name="ray0start">光線ray0の始点</param>
    /// <param name="ray0dir">光線ray0の方向ベクトル</param>
    /// <param name="pc">円の中心点の位置ベクトル</param>
    /// <param name="r">円の半径</param>
    /// <returns>光線ray0と円が交差しているならtrue,してないならfalse</returns>
    static bool RayCircleCollision(Vector2& result1, Vector2& result2, bool& result_isInsideCircle,
        Vector2 ray0start, Vector2 ray0dir, Vector2 pc, float r)
    {
        Vector2 vc0 = ray0start - pc; // 円の中心pc→レイの始点ray0startへ向かうベクトル
        Vector2 e0 = ray0dir.normalized(); // 光線ray0方向dirの単位ベクトル
        float vc0_dot_e0 = dot(vc0, e0);
        float vc0_sqrMag = vc0.sqrMagnitude(); //|vc0|の2乗
        float dif_vc0_vc0_r_r = vc0_sqrMag - r * r; //↓|vc0|の2乗 - rの2乗
        float D = vc0_dot_e0 * vc0_dot_e0 - dif_vc0_vc0_r_r;
        if (dif_vc0_vc0_r_r < 0) // |vc0|の2乗 - rの2乗 < 0のときは円の内側に交点ray0の始点がある
            result_isInsideCircle = true; // レイの始点が円の内側なのでtrue判定を返す
        else
            result_isInsideCircle = false; // レイの始点が円の外側なのでfalse判定を返す

        if (D < 0) return false; // D < 0なら光線ray0は円とぶつからない

        float sqrD = std::sqrtf(D); // √D
        float t1 = -vc0_dot_e0 - sqrD;
        float t2 = -vc0_dot_e0 + sqrD;
        if (dif_vc0_vc0_r_r < 0) // |vc0|の2乗 - rの2乗 < 0のときは円の内側に交点ray0の始点があるので
        {   // 円の内側のときは t1 と t2 の±をひっくり返す
            t1 = -vc0_dot_e0 + sqrD; // t1とt2の＋と－をひっくり返す(とresult1が最初に交わる点扱いになる)
            t2 = -vc0_dot_e0 - sqrD;
        }

        result1 = ray0start + t1 * e0; // D == 0 のときは1,2両方同じになり交点は一つ
        result2 = ray0start + t2 * e0;
        return true; // 光線ray0は円と交わる(D > 0なら2点交わり、D == 0なら1点交わる)
    }

};

#endif

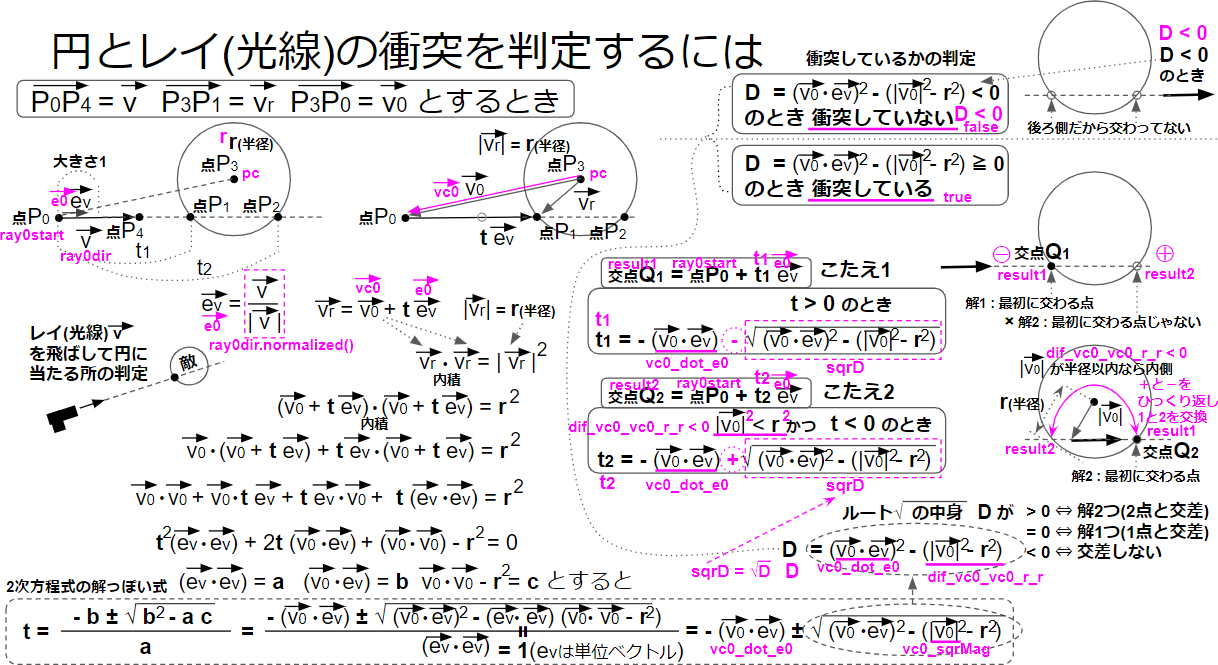
下図で上記コードの式との対応関係を確認してみてください。dif_vc0_vc0_r_r < 0 つまり|vc0|の2乗が半径rの2乗より小さい(円の内側)ときは t1 と t2 の√の±をひっくり返しています。
t1 の－√D と +√D の－のほうが最初に円と交わる点なのですが、円の内側の場合は+√Dのほうが最初に交わる点に変わっちゃうので、そのために±をひっくり返しています。

main.cppを一旦、まっさらにリセットしましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // line0
        Vector2 p0{ 5,5 }; // line0の始点
        Vector2 p1{ 15,11 }; // line0の終点
        // 線分line1
        Vector2 p2{ 5,10 };
        Vector2 p3{ 15,6 };
        float r = 1.0f; // 円の半径r 始点p2が円(青ボール)の場合を想定

        Vector2 Q; // line0とline1の交点
        Vector2 R; // line0を壁wall0とした場合のline1の終点p3の壁line0に対する反射点Rと交点Qを求める
        bool isCollision01 = MyMath::LineReflection(R, Q, p0, p1, p2, p3, r);

        mathGraph.DrawCircle(p2.x, p2.y, r, GetColor(0, 0, 255), FALSE); // 円p2(始点)を描く
        mathGraph.DrawCircle(Q.x, Q.y, r, GetColor(255, 165, 0), FALSE); // 円Q(衝突位置)を描く
        mathGraph.DrawCircle(R.x, R.y, r, GetColor(255, 255, 0), FALSE); // 円R(反射位置)を描く

        mathGraph.DrawArrow(p0.x, p0.y, 0, 0, p1.x, p1.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line0
        mathGraph.DrawArrow(p2.x, p2.y, 0, 0, p3.x, p3.y, 0.8f, 1.0f, (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255)); // 線分line1

        // 反射ベクトル(交点Q→反射点R)を描く
        if (isCollision01)
            mathGraph.DrawArrow(Q.x, Q.y, 0, 0, R.x, R.y, 0.8f, 1.0f, GetColor(255, 255, 0));

        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        mathGraph.DrawPoint(p3.x, p3.y, 3, GetColor(0, 255, 255), TRUE);
        std::string p3_String = "p3=(" + std::to_string((int)p3.x) + "," + std::to_string((int)p3.y) + ")";
        mathGraph.DrawString(p3.x, p3.y, p3_String.c_str(), GetColor(0, 255, 255));

        mathGraph.DrawPoint(Q.x, Q.y, 3, GetColor(255, 165, 0), TRUE);
        std::string Q_String = "Q=(" + std::to_string(Q.x) + "," + std::to_string(Q.y) + ")";
        mathGraph.DrawString(Q.x, Q.y - 10, Q_String.c_str(), GetColor(255, 165, 0));

        mathGraph.DrawPoint(R.x, R.y, 3, GetColor(255, 255, 0), TRUE);
        std::string R_String = "R=(" + std::to_string(R.x) + "," + std::to_string(R.y) + ")";
        mathGraph.DrawString(R.x, R.y - 10, R_String.c_str(), GetColor(255, 255, 0));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

main.cppを変更して、光線ray0 と円(中心点:pc 半径:r)の当たり判定と衝突した交点Q1,Q2 を求めて表示してみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // ray0光線レイ
        Vector2 ray0pos{ 1,2 }; // レイ光線の始点
        Vector2 ray0dir{ 2,1 }; // レイ光線の方向
        // 円
        Vector2 pc{ 5,5 };
        float r = 2.0f; // 円の半径r

        bool isInsideCircle = false; // レイの始点が円の内側のときはtrueになる
        Vector2 Q1, Q2; // 光線ray0と円の交点(Q1が最初に円とぶつかる点、Q2が後ろ側でぶつかる点)
        bool isCollision01 = MyMath::RayCircleCollision(Q1, Q2, isInsideCircle, ray0pos, ray0dir, pc, r);

        mathGraph.DrawCircle(pc.x, pc.y, r, GetColor(0, 0, 255), FALSE); // 円(中心点:pc)を描く
        // 光線ray0を描く
        mathGraph.DrawArrow(ray0pos.x, ray0pos.y, 0, 0, ray0pos.x + ray0dir.x, ray0pos.y + ray0dir.y, 0.8f, 1.0f,
                             (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255));

        // レイ光線の始点
        mathGraph.DrawPoint(ray0pos.x, ray0pos.y, 3, GetColor(255, 165, 0), TRUE);
        std::string ray0_String = "ray0=(" + std::to_string((int)ray0pos.x) + "," + std::to_string((int)ray0pos.y) + ")";
        mathGraph.DrawString(ray0pos.x, ray0pos.y, ray0_String.c_str(), GetColor(255, 165, 0));

        if (isCollision01)
        {
            // 交点Q1を描く(最初に交わる点)
            mathGraph.DrawPoint(Q1.x, Q1.y, 3, GetColor(255, 165, 0), TRUE);
            std::string Q1_String = "Q1=(" + std::to_string(Q1.x) + "," + std::to_string(Q1.y) + ")";
            mathGraph.DrawString(Q1.x, Q1.y-5, Q1_String.c_str(), GetColor(255, 165, 0));

            // 交点Q2を描く(後ろ側で交わる点)
            if (Q2 != Q1) // (Q2 が Q1と違う点ならば)
            {
                mathGraph.DrawPoint(Q2.x, Q2.y, 3, GetColor(255, 255, 0), TRUE);
                std::string Q2_String = "Q2=(" + std::to_string(Q2.x) + "," + std::to_string(Q2.y) + ")";
                mathGraph.DrawString(Q2.x, Q2.y-10, Q2_String.c_str(), GetColor(255, 255, 0));
            }
        }

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？光線ray0の方向に円があったときに、矢印が赤色に表示されて、最初に交わる交点Q1がオレンジ色に、後ろ側で交わる交点Q2が黄色に表示されましたか?
つぎに、円の内側にray0の始点があるときの実験もしておきましょう。

main.cppの光線ray0の始点を変更して、光線ray0の始点が円の内側にあるときに光線の始点が水色で表示されるか、実験表示してみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // ray0光線レイ
        Vector2 ray0pos{ 4,4 }; // レイ光線の始点
        Vector2 ray0dir{ 2,1 }; // レイ光線の方向
        // 円
        Vector2 pc{ 5,5 };
        float r = 2.0f; // 円の半径r

        bool isInsideCircle = false; // レイの始点が円の内側のときはtrueになる
        Vector2 Q1, Q2; // 光線ray0と円の交点(Q1が最初に円とぶつかる点、Q2が後ろ側でぶつかる点)
        bool isCollision01 = MyMath::RayCircleCollision(Q1, Q2, isInsideCircle, ray0pos, ray0dir, pc, r);

        mathGraph.DrawCircle(pc.x, pc.y, r, GetColor(0, 0, 255), FALSE); // 円(中心点:pc)を描く
        // 光線ray0を描く
        mathGraph.DrawArrow(ray0pos.x, ray0pos.y, 0, 0, ray0pos.x + ray0dir.x, ray0pos.y + ray0dir.y, 0.8f, 1.0f,
                             (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255));

        // レイ光線の始点(円の外側だったらオレンジ、円の内側だったら水色になる)
        mathGraph.DrawPoint(ray0pos.x, ray0pos.y, 3, (isInsideCircle)? GetColor(0, 255, 255) : GetColor(255, 165, 0), TRUE);
        std::string ray0_String = "ray0=(" + std::to_string((int)ray0pos.x) + "," + std::to_string((int)ray0pos.y) + ")";
        mathGraph.DrawString(ray0pos.x, ray0pos.y, ray0_String.c_str(), (isInsideCircle) ? GetColor(0, 255, 255) : GetColor(255, 165, 0));

        if (isCollision01)
        {
            // 交点Q1を描く(最初に交わる点)
            mathGraph.DrawPoint(Q1.x, Q1.y, 3, GetColor(255, 165, 0), TRUE);
            std::string Q1_String = "Q1=(" + std::to_string(Q1.x) + "," + std::to_string(Q1.y) + ")";
            mathGraph.DrawString(Q1.x, Q1.y-5, Q1_String.c_str(), GetColor(255, 165, 0));

            // 交点Q2を描く(後ろ側で交わる点)
            if (Q2 != Q1) // (Q2 が Q1と違う点ならば)
            {
                mathGraph.DrawPoint(Q2.x, Q2.y, 3, GetColor(255, 255, 0), TRUE);
                std::string Q2_String = "Q2=(" + std::to_string(Q2.x) + "," + std::to_string(Q2.y) + ")";
                mathGraph.DrawString(Q2.x, Q2.y-10, Q2_String.c_str(), GetColor(255, 255, 0));
            }
        }

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？光線ray0の始点が円の内側にあるときに、始点が水色で表示され、光線ray0の方向に円があったときに、最初に交わる交点Q1がオレンジ色に表示されましたか?
厳密には、円の内側にray0の始点があるときには、光線は黄色の点Q2とは当たっていない(始点より後ろ側にある)ので、交点Q2は isInsideCircle == false かどうかで表示させないようにしたほうがよいでしょう。

main.cppを変更して、光線ray0の始点が円の内側にあるときには交点Q2は表示しないようにしてみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // ray0光線レイ
        Vector2 ray0pos{ 1,2 }; // レイ光線の始点
        Vector2 ray0dir{ 2,1 }; // レイ光線の方向
        // 円
        Vector2 pc{ 5,5 };
        float r = 2.0f; // 円の半径r

        bool isInsideCircle = false; // レイの始点が円の内側のときはtrueになる
        Vector2 Q1, Q2; // 光線ray0と円の交点(Q1が最初に円とぶつかる点、Q2が後ろ側でぶつかる点)
        bool isCollision01 = MyMath::RayCircleCollision(Q1, Q2, isInsideCircle, ray0pos, ray0dir, pc, r);

        mathGraph.DrawCircle(pc.x, pc.y, r, GetColor(0, 0, 255), FALSE); // 円(中心点:pc)を描く
        // 光線ray0を描く
        mathGraph.DrawArrow(ray0pos.x, ray0pos.y, 0, 0, ray0pos.x + ray0dir.x, ray0pos.y + ray0dir.y, 0.8f, 1.0f,
                             (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255));

        // レイ光線の始点(円の外側だったらオレンジ、円の内側だったら水色になる)
        mathGraph.DrawPoint(ray0pos.x, ray0pos.y, 3, (isInsideCircle)? GetColor(0, 255, 255) : GetColor(255, 165, 0), TRUE);
        std::string ray0_String = "ray0=(" + std::to_string((int)ray0pos.x) + "," + std::to_string((int)ray0pos.y) + ")";
        mathGraph.DrawString(ray0pos.x, ray0pos.y, ray0_String.c_str(), (isInsideCircle) ? GetColor(0, 255, 255) : GetColor(255, 165, 0));

        if (isCollision01)
        {
            // 交点Q1を描く(最初に交わる点)
            mathGraph.DrawPoint(Q1.x, Q1.y, 3, GetColor(255, 165, 0), TRUE);
            std::string Q1_String = "Q1=(" + std::to_string(Q1.x) + "," + std::to_string(Q1.y) + ")";
            mathGraph.DrawString(Q1.x, Q1.y-5, Q1_String.c_str(), GetColor(255, 165, 0));

            // 交点Q2を描く(後ろ側で交わる点)
            if (Q2 != Q1 && isInsideCircle == false) // (Q2 が Q1と違う点で光線の始点が円の内側にはないとき)
            {
                mathGraph.DrawPoint(Q2.x, Q2.y, 3, GetColor(255, 255, 0), TRUE);
                std::string Q2_String = "Q2=(" + std::to_string(Q2.x) + "," + std::to_string(Q2.y) + ")";
                mathGraph.DrawString(Q2.x, Q2.y-10, Q2_String.c_str(), GetColor(255, 255, 0));
            }
        }

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？これで、円の内側に光線ray0の始点がある場合でも、正しくレイと円の当たり判定ができるようになりました。
ゲームで使う分には、基本は交点Q1(result1) を使うようにしていれば、円とレイの当たり判定としては十分かもしれません。
(交点Q2をあえて使うとしたら、銃で撃たれて、貫通したときのような表現のときに使うようなケースがあるかもしれません)

Matrix3x3で点を行列で平行移動(translate)させる

Matrix3x3.hを新規作成して3×3の配列[3][3]を内部に持つ行列を定義しましょう。

#ifndef MATRIX3X3_H_
#define MATRIX3X3_H_

#include "Vector2.h" // 2Dのベクトル

#include <ostream>
#include <cmath>

// 行列(3×3)　2Dにも3Dにも使う
struct Matrix3x3
{
    // 行列[行][列]の順 (行優先) https://qiita.com/suzuryo3893/items/9e543cdf8bc64dc7002a
    union
    {
        float m[3][3]{}; // 3×3の配列
        std::array<std::array<float, 3>, 3> mArr; // std::array型ベースなら少し便利
    };

    // float型のポインタへ(float*)キャストすればデータ配列 m の先頭のアドレスを返す
    inline operator float* () const { return (float*)m; }
    // float型のポインタへ(const float*)キャストすればデータ配列 m の先頭のアドレスを返す
    inline operator const float* () const { return (const float*)m; }

    // コンストラクタ
    Matrix3x3() = default;
    // コンストラクタ
    Matrix3x3(float m11, float m12, float m13,
        float m21, float m22, float m23,
        float m31, float m32, float m33)
        : m{ {m11, m12, m13}, {m21, m22, m23}, { m31, m32, m33} } {};

    // コンストラクタ (std::arrayで初期化版)
    Matrix3x3(std::array<std::array<float, 3>, 3>& matArr)
    {
        for (int j = 0; j < 3; ++j)
            for (int i = 0; i < 3; ++i)
                m[i][j] = matArr[i][j];
    }

};

// 行列の出力
inline std::ostream& operator << (std::ostream& left, const Matrix3x3& right)
{
    for (int i = 0; i < 3; ++i) {
        for (int j = 0; j < 3; ++j) {
            left << right.m[i][j];
            if (j < 3 - 1) {
                left << " ";
            }
        }
        left << std::endl;
    }
    return left;
};

#endif

基本はfloat m[3][3]{}; // 3×3の配列 のように[3][3]の配列をベースにした構造体です。
これに足し算や引き算や掛け算や割り算などの基本計算をoperatorで定義して行列の計算ができるように改造していきます。

Matrix3x3.hを変更し、operatorをオーバーロードして行列の足し算や引き算や掛け算や割り算などの基本計算を定義しましょう。

#ifndef MATRIX3X3_H_
#define MATRIX3X3_H_

#include "Vector2.h" // 2Dのベクトル

#include <ostream>
#include <cmath>

// 行列(3×3)　2Dにも3Dにも使う
struct Matrix3x3
{
    // 行列[行][列]の順 (行優先) https://qiita.com/suzuryo3893/items/9e543cdf8bc64dc7002a
    union
    {
        float m[3][3]{}; // 3×3の配列
        std::array<std::array<float, 3>, 3> mArr; // std::array型ベースなら少し便利
    };

    // float型のポインタへ(float*)キャストすればデータ配列 m の先頭のアドレスを返す
    inline operator float* () const { return (float*)m; }
    // float型のポインタへ(const float*)キャストすればデータ配列 m の先頭のアドレスを返す
    inline operator const float* () const { return (const float*)m; }

    // コンストラクタ
    Matrix3x3() = default;
    // コンストラクタ
    Matrix3x3(float m11, float m12, float m13,
        float m21, float m22, float m23,
        float m31, float m32, float m33)
        : m{ {m11, m12, m13}, {m21, m22, m23}, { m31, m32, m33} } {};

    // コンストラクタ (std::arrayで初期化版)
    Matrix3x3(std::array<std::array<float, 3>, 3>& matArr)
    {
        for (int j = 0; j < 3; ++j)
            for (int i = 0; i < 3; ++i)
                m[i][j] = matArr[i][j];
    }

    /*-----　演算子オーバーロード　-----*/

    inline Matrix3x3 operator + () const { return *this; }

    // マイナスの符号を単体の行列につけたとき
    inline Matrix3x3 operator -() const
    {
        Matrix3x3 result;
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                result.m[i][j] = -this->m[i][j];
        return result;
    };

    inline Matrix3x3& operator += (const Matrix3x3& add)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] + add.m[i][j];
        return    *this;
    }

    inline Matrix3x3& operator -= (const Matrix3x3& sub)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] - sub.m[i][j];
        return    *this;
    }

    inline Matrix3x3& operator *= (const Matrix3x3& mul)
    {
        Matrix3x3 tmp; // 値を一時保管
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                tmp.m[i][j] = this->m[i][j];

        for (int i = 0; i < 3; ++i) {
            for (int j = 0; j < 3; ++j) {
                this->m[i][j] = 0;
                for (int k = 0; k < 3; ++k)
                    this->m[i][j] += tmp.m[i][k] * mul.m[k][j];
            }
        }
        return    *this;
    }

    inline Matrix3x3& operator *= (float multiply_num)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] * multiply_num;
        return    *this;
    }

    inline Matrix3x3& operator /= (float divide_num)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] / divide_num;
        return    *this;
    }

    // 一致演算子行列の中身が全部一致するか一つでも違えばfalse
    inline bool operator == (const Matrix3x3& other)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                if (this->m[i][j] != other.m[i][j]) return false;
        return    true;
    }

    // 不一致演算子
    inline bool operator != (const Matrix3x3& other)
    {
        return    !(*this == other);
    }

};

// 行列の加算
inline Matrix3x3 operator + (const Matrix3x3& left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left.m[i][j] + right.m[i][j];

    return result;
};

// 行列の減算
inline Matrix3x3 operator - (const Matrix3x3& left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left.m[i][j] - right.m[i][j];

    return result;
};

// 行列のスカラー倍 (スカラー×行列）
inline Matrix3x3 operator * (float left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left * right.m[i][j];

    return result;
};

// 行列のスカラー倍 (行列×スカラー）
inline Matrix3x3 operator * (const Matrix3x3& left, float right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left.m[i][j] * right;

    return result;
};

// 行列の積
inline Matrix3x3 operator * (const Matrix3x3& left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i) {
        for (int j = 0; j < 3; ++j) {
            result.m[i][j] = 0;
            for (int k = 0; k < 3; ++k)
                result.m[i][j] += left.m[i][k] * right.m[k][j];
        }
    }
    return result;
};

//[2D]ベクトルと行列の積
inline Vector2 operator * (const Vector2& left, const Matrix3x3& right)
{
    float x = left.x * right.m[0][0] + left.y * right.m[1][0] + right.m[2][0];
    float y = left.x * right.m[0][1] + left.y * right.m[1][1] + right.m[2][1];
    return Vector2{ x, y };
};

inline const Matrix3x3 operator / (const Matrix3x3& left, const float right)
{
    return left * (1.0f / right);
}

// 行列の出力
inline std::ostream& operator << (std::ostream& left, const Matrix3x3& right)
{
    for (int i = 0; i < 3; ++i) {
        for (int j = 0; j < 3; ++j) {
            left << right.m[i][j];
            if (j < 3 - 1) {
                left << " ";
            }
        }
        left << std::endl;
    }
    return left;
};

#endif

これで行列の足し算や引き算や掛け算や割り算などの基本計算はできるようになりました。
さらに、数字における 0 や 1 などの行列版として、ゼロ行列(zero) や単位行列E(identity:アイデンティティ)も追加しておきましょう。

Matrix3x3.hを変更し、operatorをオーバーロードして行列の足し算や引き算や掛け算や割り算などの基本計算を定義しましょう。

#ifndef MATRIX3X3_H_
#define MATRIX3X3_H_

#include "Vector2.h" // 2Dのベクトル

#include <ostream>
#include <cmath>

// 行列(3×3)　2Dにも3Dにも使う
struct Matrix3x3
{
    // 行列[行][列]の順 (行優先) https://qiita.com/suzuryo3893/items/9e543cdf8bc64dc7002a
    union
    {
        float m[3][3]{}; // 3×3の配列
        std::array<std::array<float, 3>, 3> mArr; // std::array型ベースなら少し便利
    };

    // float型のポインタへ(float*)キャストすればデータ配列 m の先頭のアドレスを返す
    inline operator float* () const { return (float*)m; }
    // float型のポインタへ(const float*)キャストすればデータ配列 m の先頭のアドレスを返す
    inline operator const float* () const { return (const float*)m; }

    // コンストラクタ
    Matrix3x3() = default;
    // コンストラクタ
    Matrix3x3(float m11, float m12, float m13,
        float m21, float m22, float m23,
        float m31, float m32, float m33)
        : m{ {m11, m12, m13}, {m21, m22, m23}, { m31, m32, m33} } {};

    // コンストラクタ (std::arrayで初期化版)
    Matrix3x3(std::array<std::array<float, 3>, 3>& matArr)
    {
        for (int j = 0; j < 3; ++j)
            for (int i = 0; i < 3; ++i)
                m[i][j] = matArr[i][j];
    }

    // ゼロ行列を返す
    static Matrix3x3 zero()
    {
        return Matrix3x3{ 0.0f, 0.0f, 0.0f,
                          0.0f, 0.0f, 0.0f,
                          0.0f, 0.0f, 0.0f };
    };

    // 単位行列を返す
    static Matrix3x3 identity()
    {
        return Matrix3x3{ 1.0f, 0.0f, 0.0f,
                          0.0f, 1.0f, 0.0f,
                          0.0f, 0.0f, 1.0f };
    };

    /*-----　演算子オーバーロード　-----*/

    inline Matrix3x3 operator + () const { return *this; }

    // マイナスの符号を単体の行列につけたとき
    inline Matrix3x3 operator -() const
    {
        Matrix3x3 result;
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                result.m[i][j] = -this->m[i][j];
        return result;
    };

    inline Matrix3x3& operator += (const Matrix3x3& add)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] + add.m[i][j];
        return    *this;
    }

    inline Matrix3x3& operator -= (const Matrix3x3& sub)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] - sub.m[i][j];
        return    *this;
    }

    inline Matrix3x3& operator *= (const Matrix3x3& mul)
    {
        Matrix3x3 tmp; // 値を一時保管
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                tmp.m[i][j] = this->m[i][j];

        for (int i = 0; i < 3; ++i) {
            for (int j = 0; j < 3; ++j) {
                this->m[i][j] = 0;
                for (int k = 0; k < 3; ++k)
                    this->m[i][j] += tmp.m[i][k] * mul.m[k][j];
            }
        }
        return    *this;
    }

    inline Matrix3x3& operator *= (float multiply_num)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] * multiply_num;
        return    *this;
    }

    inline Matrix3x3& operator /= (float divide_num)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] / divide_num;
        return    *this;
    }

    // 一致演算子行列の中身が全部一致するか一つでも違えばfalse
    inline bool operator == (const Matrix3x3& other)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                if (this->m[i][j] != other.m[i][j]) return false;
        return    true;
    }

    // 不一致演算子
    inline bool operator != (const Matrix3x3& other)
    {
        return    !(*this == other);
    }

};

// 行列の加算
inline Matrix3x3 operator + (const Matrix3x3& left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left.m[i][j] + right.m[i][j];

    return result;
};

// 行列の減算
inline Matrix3x3 operator - (const Matrix3x3& left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left.m[i][j] - right.m[i][j];

    return result;
};

// 行列のスカラー倍 (スカラー×行列）
inline Matrix3x3 operator * (float left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left * right.m[i][j];

    return result;
};

// 行列のスカラー倍 (行列×スカラー）
inline Matrix3x3 operator * (const Matrix3x3& left, float right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left.m[i][j] * right;

    return result;
};

// 行列の積
inline Matrix3x3 operator * (const Matrix3x3& left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i) {
        for (int j = 0; j < 3; ++j) {
            result.m[i][j] = 0;
            for (int k = 0; k < 3; ++k)
                result.m[i][j] += left.m[i][k] * right.m[k][j];
        }
    }
    return result;
};

//[2D]ベクトルと行列の積
inline Vector2 operator * (const Vector2& left, const Matrix3x3& right)
{
    float x = left.x * right.m[0][0] + left.y * right.m[1][0] + right.m[2][0];
    float y = left.x * right.m[0][1] + left.y * right.m[1][1] + right.m[2][1];
    return Vector2{ x, y };
};

inline const Matrix3x3 operator / (const Matrix3x3& left, const float right)
{
    return left * (1.0f / right);
}

// 行列の出力
inline std::ostream& operator << (std::ostream& left, const Matrix3x3& right)
{
    for (int i = 0; i < 3; ++i) {
        for (int j = 0; j < 3; ++j) {
            left << right.m[i][j];
            if (j < 3 - 1) {
                left << " ";
            }
        }
        left << std::endl;
    }
    return left;
};

#endif

これで行列の基本計算は万全になりました。
それではためしに、点(位置ベクトル) に平行移動行列を掛け算して、点の位置を行列の計算を通して平行移動させてみましょう。

main.cppを一旦、きれいにまっさらにリセットしましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        // ray0光線レイ
        Vector2 ray0pos{ 1,2 }; // レイ光線の始点
        Vector2 ray0dir{ 2,1 }; // レイ光線の方向
        // 円
        Vector2 pc{ 5,5 };
        float r = 2.0f; // 円の半径r

        bool isInsideCircle = false; // レイの始点が円の内側のときはtrueになる
        Vector2 Q1, Q2; // 光線ray0と円の交点(Q1が最初に円とぶつかる点、Q2が後ろ側でぶつかる点)
        bool isCollision01 = MyMath::RayCircleCollision(Q1, Q2, isInsideCircle, ray0pos, ray0dir, pc, r);

        mathGraph.DrawCircle(pc.x, pc.y, r, GetColor(0, 0, 255), FALSE); // 円(中心点:pc)を描く
        // 光線ray0を描く
        mathGraph.DrawArrow(ray0pos.x, ray0pos.y, 0, 0, ray0pos.x + ray0dir.x, ray0pos.y + ray0dir.y, 0.8f, 1.0f,
                             (isCollision01) ? GetColor(255, 0, 0) : GetColor(255, 255, 255));

        // レイ光線の始点(円の外側だったらオレンジ、円の内側だったら水色になる)
        mathGraph.DrawPoint(ray0pos.x, ray0pos.y, 3, (isInsideCircle)? GetColor(0, 255, 255) : GetColor(255, 165, 0), TRUE);
        std::string ray0_String = "ray0=(" + std::to_string((int)ray0pos.x) + "," + std::to_string((int)ray0pos.y) + ")";
        mathGraph.DrawString(ray0pos.x, ray0pos.y, ray0_String.c_str(), (isInsideCircle) ? GetColor(0, 255, 255) : GetColor(255, 165, 0));

        if (isCollision01)
        {
            // 交点Q1を描く(最初に交わる点)
            mathGraph.DrawPoint(Q1.x, Q1.y, 3, GetColor(255, 165, 0), TRUE);
            std::string Q1_String = "Q1=(" + std::to_string(Q1.x) + "," + std::to_string(Q1.y) + ")";
            mathGraph.DrawString(Q1.x, Q1.y-5, Q1_String.c_str(), GetColor(255, 165, 0));

            // 交点Q2を描く(後ろ側で交わる点)
            if (Q2 != Q1 && isInsideCircle == false) // (Q2 が Q1と違う点で光線の始点が円の内側にはないとき)
            {
                mathGraph.DrawPoint(Q2.x, Q2.y, 3, GetColor(255, 255, 0), TRUE);
                std::string Q2_String = "Q2=(" + std::to_string(Q2.x) + "," + std::to_string(Q2.y) + ")";
                mathGraph.DrawString(Q2.x, Q2.y-10, Q2_String.c_str(), GetColor(255, 255, 0));
            }
        }

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

main.cppを変更して、点p0{1,1} を 平行移動行列(translate:トランスレート) で x方向に+2 y方向に+3 平行移動してみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "Matrix3x3.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p0{ 1,1 }; // 点p0

        Matrix3x3 translate{ 1,0,0,
                             0,1,0,
                             2,3,1 }; // 平行移動行列

        // 点p1
        Vector2 p1 = p0 * translate; // 点p0×translate (平行移動行列を右から掛け算)すると平行移動する

        // 矢印p0→p1を描く
        mathGraph.DrawArrow(p0.x, p0.y, 0, 0, p1.x, p1.y, 0.8f, 1.0f, GetColor(255, 255, 255));

        // 点p0を描く
        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 255, 255), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 255, 255));

        // 点p1を描く
        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(255, 0, 0));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？行列の左下の方の 2,3 の数字が効いて、点p0{1,1} が {+2,+3} 移動して { 1+2, 1+3 } = { 3,4 }に移動したでしょうか？
では、今度はこの数字を{ +4, +5 }に変えて実験してみましょう。

main.cppを変更して、点p0{1,1} を平行移動行列(translate:トランスレート) で x方向に+4 y方向に+5 平行移動してみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "Matrix3x3.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p0{ 1,1 }; // 点p0

        Matrix3x3 translate{ 1,0,0,
                             0,1,0,
                             4,5,1 }; // 平行移動行列

        // 点p1
        Vector2 p1 = p0 * translate; // 点p0×translate (平行移動行列を右から掛け算)すると平行移動する

        // 矢印p0→p1を描く
        mathGraph.DrawArrow(p0.x, p0.y, 0, 0, p1.x, p1.y, 0.8f, 1.0f, GetColor(255, 255, 255));

        // 点p0を描く
        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 255, 255), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 255, 255));

        // 点p1を描く
        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(255, 0, 0));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？こんどは行列の左下の方の 4,5 の数字が効いて、点p0{1,1} が {+4,+5} 移動して { 1+4, 1+5 } = { 5,6 }に移動したでしょうか？
このように3×3の行列の左下の2か所は「平行移動成分」となっていますので、この[2][0]、[2][1]すなわち2行目0列、2行目1列の数字を取り出したり書き換えたりすれば、
平行移動する移動先を操作することができるのです。このように行列の各箇所にはゲームを描画する際に、点がどのように移動するかなどの数値情報の「成分」が入っているわけです。
ただし、要注意なのは、DXライブラリは「DirectX」をベースにした3D行列での描画を採用しています(UnityもDirectX系)が、
ネット上には3D描画行列の例として「OpenGL系」をベースにした3D行列でゲームを作成している例も沢山載っています。
この「OpenGL系」をベースにした3D行列の場合は「行と列が逆になります！！」ので以下のような行列が平行移動の行列となってしまいます。

        Matrix3x3 translate{ 1,0,3,
                             0,1,4,
                             0,0,1 }; // 平行移動行列{+3,+4}(OpenGL系)

はい、位置が斜め方向 1,1,1 を境にして逆ですね。
このように、「DirectX」をベースにした3D行列を「OpenGL系」をベースにした3D行列に使うためには数字の位置の「転置(tranpose:トランポーズ)」が必要になります。
つまり、計算の過程で数値の位置を斜め方向に鏡のように逆にする「転置」の処理が必要になることがあります。
このために、Matrix3x3.hに「転置」処理としてtranspose関数も準備しておきましょう。

Matrix3x3.hを変更し、転置処理をするtranspose関数を定義しましょう。
ついでに毎回、手打ちで平行移動行列を定義しなくて済むように平行移動行列を返すtranslate関数(DirectX系対応ver.)も定義して便利にしておきましょう。

#ifndef MATRIX3X3_H_
#define MATRIX3X3_H_

#include "Vector2.h" // 2Dのベクトル

#include <ostream>
#include <cmath>

// 行列(3×3)　2Dにも3Dにも使う
struct Matrix3x3
{
    // 行列[行][列]の順 (行優先) https://qiita.com/suzuryo3893/items/9e543cdf8bc64dc7002a
    union
    {
        float m[3][3]{}; // 3×3の配列
        std::array<std::array<float, 3>, 3> mArr; // std::array型ベースなら少し便利
    };

    // float型のポインタへ(float*)キャストすればデータ配列 m の先頭のアドレスを返す
    inline operator float* () const { return (float*)m; }
    // float型のポインタへ(const float*)キャストすればデータ配列 m の先頭のアドレスを返す
    inline operator const float* () const { return (const float*)m; }

    // コンストラクタ
    Matrix3x3() = default;
    // コンストラクタ
    Matrix3x3(float m11, float m12, float m13,
        float m21, float m22, float m23,
        float m31, float m32, float m33)
        : m{ {m11, m12, m13}, {m21, m22, m23}, { m31, m32, m33} } {};

    // コンストラクタ (std::arrayで初期化版)
    Matrix3x3(std::array<std::array<float, 3>, 3>& matArr)
    {
        for (int j = 0; j < 3; ++j)
            for (int i = 0; i < 3; ++i)
                m[i][j] = matArr[i][j];
    }

    // ゼロ行列を返す
    static Matrix3x3 zero()
    {
        return Matrix3x3{ 0.0f, 0.0f, 0.0f,
                          0.0f, 0.0f, 0.0f,
                          0.0f, 0.0f, 0.0f };
    };

    // 単位行列を返す
    static Matrix3x3 identity()
    {
        return Matrix3x3{ 1.0f, 0.0f, 0.0f,
                          0.0f, 1.0f, 0.0f,
                          0.0f, 0.0f, 1.0f };
    };

    //[2D]平行移動行列を返す(2D向け) (DirectX系)
    static Matrix3x3 translate(const Vector2& t)
    {
        return Matrix3x3{ 1.0, 0.0f, 0.0f,
                          0.0, 1.0f, 0.0f,
                          t.x, t.y, 1.0f };
    };

    // 転置行列を返す(メンバ関数版)
    inline Matrix3x3 transpose()
    {
        Matrix3x3 result;
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                result.m[i][j] = this->m[j][i]; // 行i と列j を行j と列i に交換

        return result;
    };

    /*-----　演算子オーバーロード　-----*/

    inline Matrix3x3 operator + () const { return *this; }

    // マイナスの符号を単体の行列につけたとき
    inline Matrix3x3 operator -() const
    {
        Matrix3x3 result;
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                result.m[i][j] = -this->m[i][j];
        return result;
    };

    inline Matrix3x3& operator += (const Matrix3x3& add)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] + add.m[i][j];
        return    *this;
    }

    inline Matrix3x3& operator -= (const Matrix3x3& sub)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] - sub.m[i][j];
        return    *this;
    }

    inline Matrix3x3& operator *= (const Matrix3x3& mul)
    {
        Matrix3x3 tmp; // 値を一時保管
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                tmp.m[i][j] = this->m[i][j];

        for (int i = 0; i < 3; ++i) {
            for (int j = 0; j < 3; ++j) {
                this->m[i][j] = 0;
                for (int k = 0; k < 3; ++k)
                    this->m[i][j] += tmp.m[i][k] * mul.m[k][j];
            }
        }
        return    *this;
    }

    inline Matrix3x3& operator *= (float multiply_num)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] * multiply_num;
        return    *this;
    }

    inline Matrix3x3& operator /= (float divide_num)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] / divide_num;
        return    *this;
    }

    // 一致演算子行列の中身が全部一致するか一つでも違えばfalse
    inline bool operator == (const Matrix3x3& other)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                if (this->m[i][j] != other.m[i][j]) return false;
        return    true;
    }

    // 不一致演算子
    inline bool operator != (const Matrix3x3& other)
    {
        return    !(*this == other);
    }

};

// 行列の加算
inline Matrix3x3 operator + (const Matrix3x3& left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left.m[i][j] + right.m[i][j];

    return result;
};

// 行列の減算
inline Matrix3x3 operator - (const Matrix3x3& left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left.m[i][j] - right.m[i][j];

    return result;
};

// 行列のスカラー倍 (スカラー×行列）
inline Matrix3x3 operator * (float left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left * right.m[i][j];

    return result;
};

// 行列のスカラー倍 (行列×スカラー）
inline Matrix3x3 operator * (const Matrix3x3& left, float right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left.m[i][j] * right;

    return result;
};

// 行列の積
inline Matrix3x3 operator * (const Matrix3x3& left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i) {
        for (int j = 0; j < 3; ++j) {
            result.m[i][j] = 0;
            for (int k = 0; k < 3; ++k)
                result.m[i][j] += left.m[i][k] * right.m[k][j];
        }
    }
    return result;
};

//[2D]ベクトルと行列の積
inline Vector2 operator * (const Vector2& left, const Matrix3x3& right)
{
    float x = left.x * right.m[0][0] + left.y * right.m[1][0] + right.m[2][0];
    float y = left.x * right.m[0][1] + left.y * right.m[1][1] + right.m[2][1];
    return Vector2{ x, y };
};

inline const Matrix3x3 operator / (const Matrix3x3& left, const float right)
{
    return left * (1.0f / right);
}

// 転置行列を返す
inline Matrix3x3 transpose(const Matrix3x3& mat)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = mat.m[j][i]; // 行i と列j を行j と列i に交換

    return result;
};

// 行列の出力
inline std::ostream& operator << (std::ostream& left, const Matrix3x3& right)
{
    for (int i = 0; i < 3; ++i) {
        for (int j = 0; j < 3; ++j) {
            left << right.m[i][j];
            if (j < 3 - 1) {
                left << " ";
            }
        }
        left << std::endl;
    }
    return left;
};

#endif

では、平行移動行列を返すtranslate関数(DirectX系対応ver.)を利用して、main.cppで点を手軽に平行移動してみましょう。

main.cppを変更して、点p0{1,1} を平行移動行列をtranslate関数を使って初期化して x方向に+4 y方向に+5 平行移動してみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "Matrix3x3.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p0{ 1,1 }; // 点p0

        Matrix3x3 translate{ 1,0,0,
                             0,1,0,
                             4,5,1 }; // 平行移動行列
        Matrix3x3 translate = Matrix3x3::translate(Vector2{ 4,5 }); // 平行移動行列

        // 点p1
        Vector2 p1 = p0 * translate; // 点p0×translate (平行移動行列を右から掛け算)すると平行移動する

        // 矢印p0→p1を描く
        mathGraph.DrawArrow(p0.x, p0.y, 0, 0, p1.x, p1.y, 0.8f, 1.0f, GetColor(255, 255, 255));

        // 点p0を描く
        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 255, 255), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 255, 255));

        // 点p1を描く
        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(255, 0, 0));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？translate関数を使えば、手打ちで行列を3行ぶん書くよりは手軽に平行移動の行列をゲットすることができますね。
ただし、勉強のためには、ちゃんと1回は自分で行列を「手で打つ」練習をしておかないと、行列って何??というのがわからないままになっちゃいます。
行列をイメージできないまま使うのではなく、実際の3x3の行列をイメージして、数値データをイメージして使うことが勉強としては大事です。
そうでなければ、例えば、DirectX系の環境なのに、OpenGL系のネット上のプログラムサンプルを使ってしまったときに、
行列の中身の数字を見て「数値の要素がひっくり返っている」ことになかなか気づけない状況になったりすることがあるかもしれません。
便利なものを「基礎知識」があるうえで使いこなすのと「もやもやを抱えたまま、よく知らないままただ使う」のとは全然違うということです。

Matrix3x3で点を行列でスケール(拡大縮小)させる

main.cppを変更して、点p0{1,1} を スケール行列{×3倍,×4倍}を使って、x方向に×3倍 y方向に×4倍スケーリングしてみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "Matrix3x3.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p0{ 1,1 }; // 点p0

        Matrix3x3 scale{ 2,0,0,
                         0,3,0,
                         0,0,1 }; // スケール(拡大縮小)行列
        Matrix3x3 translate = Matrix3x3::translate(Vector2{ 4,5 }); // 平行移動行列

        // 点p1
        Vector2 p1 = p0 * scale; // 点p0×scale (スケール行列を右から掛け算)すると拡大縮小する

        // 矢印p0→p1を描く
        mathGraph.DrawArrow(p0.x, p0.y, 0, 0, p1.x, p1.y, 0.8f, 1.0f, GetColor(255, 255, 255));

        // 点p0を描く
        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 255, 255), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 255, 255));

        // 点p1を描く
        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(255, 0, 0));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？今回は、行列の斜め方向成分の 1,1,1 を 2,3,1 にすることで点の位置をx方向に2倍、y方向に3倍することができることが実感できたでしょうか?
1点だけだとあまり、スケールアップした実感がわかないかもしれませんので、こんどは3点をまとめてスケールアップして三角形をスケールアップしてみましょう。

main.cppを一旦、きれいにまっさらにリセットしましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "Matrix3x3.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p0{ 1,1 }; // 点p0

        Matrix3x3 scale{ 2,0,0,
                         0,3,0,
                         0,0,1 }; // スケール(拡大縮小)行列

        // 点p1
        Vector2 p1 = p0 * scale; // 点p0×scale (スケール行列を右から掛け算)すると拡大縮小する

        // 矢印p0→p1を描く
        mathGraph.DrawArrow(p0.x, p0.y, 0, 0, p1.x, p1.y, 0.8f, 1.0f, GetColor(255, 255, 255));

        // 点p0を描く
        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 255, 255), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 255, 255));

        // 点p1を描く
        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(255, 0, 0));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

main.cppを変更して、3点p0{1,1} 点p1{3,4} 点p2{5,2} を スケール行列{×2倍,×5倍}を使って、x方向に×2倍 y方向に×5倍スケーリングしてみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "Matrix3x3.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p0{ 1,1 }; // 点p0
        Vector2 p1{ 3,4 }; // 点p1
        Vector2 p2{ 5,2 }; // 点p2

        Matrix3x3 scale{ 2,0,0,
                         0,5,0,
                         0,0,1 }; // スケール(拡大縮小)行列

        // 点q0,q1,q2
        Vector2 q0 = p0 * scale; // 点p0×scale (スケール行列を右から掛け算)すると拡大縮小する
        Vector2 q1 = p1 * scale; // 点p1×scale (スケール行列を右から掛け算)すると拡大縮小する
        Vector2 q2 = p2 * scale; // 点p2×scale (スケール行列を右から掛け算)すると拡大縮小する

        // 三角形p0,p1,p2を描く
        mathGraph.DrawLine(p0.x, p0.y, p1.x, p1.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(p1.x, p1.y, p2.x, p2.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(p2.x, p2.y, p0.x, p0.y, GetColor(255, 255, 255));

        // スケール後の三角形q0,q1,q2を描く
        mathGraph.DrawLine(q0.x, q0.y, q1.x, q1.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(q1.x, q1.y, q2.x, q2.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(q2.x, q2.y, q0.x, q0.y, GetColor(255, 255, 255));

        // スケール前の3点を描く

        // 点p0を描く
        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        // 点p1を描く
        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        // 点p2を描く
        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        // スケールしたあとの3点を描く

        // 点q0を描く
        mathGraph.DrawPoint(q0.x, q0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string q0_String = "q0=(" + std::to_string(q0.x) + "," + std::to_string(q0.y) + ")";
        mathGraph.DrawString(q0.x, q0.y, q0_String.c_str(), GetColor(255, 0, 0));

        // 点q1を描く
        mathGraph.DrawPoint(q1.x, q1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string q1_String = "q1=(" + std::to_string(q1.x) + "," + std::to_string(q1.y) + ")";
        mathGraph.DrawString(q1.x, q1.y, q1_String.c_str(), GetColor(0, 255, 0));

        // 点q2を描く
        mathGraph.DrawPoint(q2.x, q2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string q2_String = "q2=(" + std::to_string(q2.x) + "," + std::to_string(q2.y) + ")";
        mathGraph.DrawString(q2.x, q2.y, q2_String.c_str(), GetColor(0, 0, 255));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？三角形をスケーリングすることで拡大していることが実感できたでしょうか?
xとyの拡大率が違うので、もとの三角形と比べて、縦方向にぐいーんとゆがんでスケーリングされていることにも着目しておいてください。

では、今回も今後を手軽にするために、Matrix3x3.hにスケール行列を得る関数を追加して行列の数字を全部は手打ちせずにスケーリング行列をゲットできるようにしておきましょう。

Matrix3x3.hを変更してスケール行列をゲットするためのscale関数を定義しましょう。

#ifndef MATRIX3X3_H_
#define MATRIX3X3_H_

#include "Vector2.h" // 2Dのベクトル

#include <ostream>
#include <cmath>

// 行列(3×3)　2Dにも3Dにも使う
struct Matrix3x3
{
    // 行列[行][列]の順 (行優先) https://qiita.com/suzuryo3893/items/9e543cdf8bc64dc7002a
    union
    {
        float m[3][3]{}; // 3×3の配列
        std::array<std::array<float, 3>, 3> mArr; // std::array型ベースなら少し便利
    };

    // float型のポインタへ(float*)キャストすればデータ配列 m の先頭のアドレスを返す
    inline operator float* () const { return (float*)m; }
    // float型のポインタへ(const float*)キャストすればデータ配列 m の先頭のアドレスを返す
    inline operator const float* () const { return (const float*)m; }

    // コンストラクタ
    Matrix3x3() = default;
    // コンストラクタ
    Matrix3x3(float m11, float m12, float m13,
        float m21, float m22, float m23,
        float m31, float m32, float m33)
        : m{ {m11, m12, m13}, {m21, m22, m23}, { m31, m32, m33} } {};

    // コンストラクタ (std::arrayで初期化版)
    Matrix3x3(std::array<std::array<float, 3>, 3>& matArr)
    {
        for (int j = 0; j < 3; ++j)
            for (int i = 0; i < 3; ++i)
                m[i][j] = matArr[i][j];
    }

    // ゼロ行列を返す
    static Matrix3x3 zero()
    {
        return Matrix3x3{ 0.0f, 0.0f, 0.0f,
                          0.0f, 0.0f, 0.0f,
                          0.0f, 0.0f, 0.0f };
    };

    // 単位行列を返す
    static Matrix3x3 identity()
    {
        return Matrix3x3{ 1.0f, 0.0f, 0.0f,
                          0.0f, 1.0f, 0.0f,
                          0.0f, 0.0f, 1.0f };
    };

    //[2D]拡大縮小行列を返す(2D向け)
    static Matrix3x3 scale(const Vector2& s)
    {
        return Matrix3x3{ s.x, 0.0f, 0.0f,
                          0.0f, s.y, 0.0f,
                          0.0f, 0.0f, 1.0f };
    };

    //[2D]平行移動行列を返す(2D向け) (DirectX系)
    static Matrix3x3 translate(const Vector2& t)
    {
        return Matrix3x3{ 1.0, 0.0f, 0.0f,
                          0.0, 1.0f, 0.0f,
                          t.x, t.y, 1.0f };
    };

    // 転置行列を返す(メンバ関数版)
    inline Matrix3x3 transpose()
    {
        Matrix3x3 result;
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                result.m[i][j] = this->m[j][i]; // 行i と列j を行j と列i に交換

        return result;
    };

    /*-----　演算子オーバーロード　-----*/

    inline Matrix3x3 operator + () const { return *this; }

    // マイナスの符号を単体の行列につけたとき
    inline Matrix3x3 operator -() const
    {
        Matrix3x3 result;
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                result.m[i][j] = -this->m[i][j];
        return result;
    };

    inline Matrix3x3& operator += (const Matrix3x3& add)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] + add.m[i][j];
        return    *this;
    }

    inline Matrix3x3& operator -= (const Matrix3x3& sub)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] - sub.m[i][j];
        return    *this;
    }

    inline Matrix3x3& operator *= (const Matrix3x3& mul)
    {
        Matrix3x3 tmp; // 値を一時保管
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                tmp.m[i][j] = this->m[i][j];

        for (int i = 0; i < 3; ++i) {
            for (int j = 0; j < 3; ++j) {
                this->m[i][j] = 0;
                for (int k = 0; k < 3; ++k)
                    this->m[i][j] += tmp.m[i][k] * mul.m[k][j];
            }
        }
        return    *this;
    }

    inline Matrix3x3& operator *= (float multiply_num)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] * multiply_num;
        return    *this;
    }

    inline Matrix3x3& operator /= (float divide_num)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] / divide_num;
        return    *this;
    }

    // 一致演算子行列の中身が全部一致するか一つでも違えばfalse
    inline bool operator == (const Matrix3x3& other)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                if (this->m[i][j] != other.m[i][j]) return false;
        return    true;
    }

    // 不一致演算子
    inline bool operator != (const Matrix3x3& other)
    {
        return    !(*this == other);
    }

};

// 行列の加算
inline Matrix3x3 operator + (const Matrix3x3& left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left.m[i][j] + right.m[i][j];

    return result;
};

// 行列の減算
inline Matrix3x3 operator - (const Matrix3x3& left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left.m[i][j] - right.m[i][j];

    return result;
};

// 行列のスカラー倍 (スカラー×行列）
inline Matrix3x3 operator * (float left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left * right.m[i][j];

    return result;
};

// 行列のスカラー倍 (行列×スカラー）
inline Matrix3x3 operator * (const Matrix3x3& left, float right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left.m[i][j] * right;

    return result;
};

// 行列の積
inline Matrix3x3 operator * (const Matrix3x3& left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i) {
        for (int j = 0; j < 3; ++j) {
            result.m[i][j] = 0;
            for (int k = 0; k < 3; ++k)
                result.m[i][j] += left.m[i][k] * right.m[k][j];
        }
    }
    return result;
};

//[2D]ベクトルと行列の積
inline Vector2 operator * (const Vector2& left, const Matrix3x3& right)
{
    float x = left.x * right.m[0][0] + left.y * right.m[1][0] + right.m[2][0];
    float y = left.x * right.m[0][1] + left.y * right.m[1][1] + right.m[2][1];
    return Vector2{ x, y };
};

inline const Matrix3x3 operator / (const Matrix3x3& left, const float right)
{
    return left * (1.0f / right);
}

// 転置行列を返す
inline Matrix3x3 transpose(const Matrix3x3& mat)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = mat.m[j][i]; // 行i と列j を行j と列i に交換

    return result;
};

// 行列の出力
inline std::ostream& operator << (std::ostream& left, const Matrix3x3& right)
{
    for (int i = 0; i < 3; ++i) {
        for (int j = 0; j < 3; ++j) {
            left << right.m[i][j];
            if (j < 3 - 1) {
                left << " ";
            }
        }
        left << std::endl;
    }
    return left;
};

#endif

main.cppを変更して、3点p0{1,1} 点p1{3,4} 点p2{5,2} を scale関数でゲットしたスケール行列{×2倍,×5倍}を使って、x方向に×2倍 y方向に×5倍スケーリングしてみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "Matrix3x3.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p0{ 1,1 }; // 点p0
        Vector2 p1{ 3,4 }; // 点p1
        Vector2 p2{ 5,2 }; // 点p2

        Matrix3x3 scale{ 2,0,0,
                         0,5,0,
                         0,0,1 }; // スケール(拡大縮小)行列
        Matrix3x3 scale = Matrix3x3::scale(Vector2{ -2,5 }); // スケール(拡大縮小)行列

        // 点q0,q1,q2
        Vector2 q0 = p0 * scale; // 点p0×scale (スケール行列を右から掛け算)すると拡大縮小する
        Vector2 q1 = p1 * scale; // 点p1×scale (スケール行列を右から掛け算)すると拡大縮小する
        Vector2 q2 = p2 * scale; // 点p2×scale (スケール行列を右から掛け算)すると拡大縮小する

        // 三角形p0,p1,p2を描く
        mathGraph.DrawLine(p0.x, p0.y, p1.x, p1.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(p1.x, p1.y, p2.x, p2.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(p2.x, p2.y, p0.x, p0.y, GetColor(255, 255, 255));

        // スケール後の三角形q0,q1,q2を描く
        mathGraph.DrawLine(q0.x, q0.y, q1.x, q1.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(q1.x, q1.y, q2.x, q2.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(q2.x, q2.y, q0.x, q0.y, GetColor(255, 255, 255));

        // スケール前の3点を描く

        // 点p0を描く
        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        // 点p1を描く
        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        // 点p2を描く
        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        // スケールしたあとの3点を描く

        // 点q0を描く
        mathGraph.DrawPoint(q0.x, q0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string q0_String = "q0=(" + std::to_string(q0.x) + "," + std::to_string(q0.y) + ")";
        mathGraph.DrawString(q0.x, q0.y, q0_String.c_str(), GetColor(255, 0, 0));

        // 点q1を描く
        mathGraph.DrawPoint(q1.x, q1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string q1_String = "q1=(" + std::to_string(q1.x) + "," + std::to_string(q1.y) + ")";
        mathGraph.DrawString(q1.x, q1.y, q1_String.c_str(), GetColor(0, 255, 0));

        // 点q2を描く
        mathGraph.DrawPoint(q2.x, q2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string q2_String = "q2=(" + std::to_string(q2.x) + "," + std::to_string(q2.y) + ")";
        mathGraph.DrawString(q2.x, q2.y, q2_String.c_str(), GetColor(0, 0, 255));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？これで手軽にスケーリング行列を得ることができるようになりました。
もう1点の注目ポイントとして、今回は{ ×2倍,×5倍 }ではなく、{ ×-2倍,×5倍 }という形でx軸方向をマイナス倍にしてみました。
x方向をマイナス倍すると、Y軸(縦軸)を鏡にして、左右が反転します。
y方向をマイナス倍すると、X軸(横軸)を鏡にして、上下が反転します。
x方向とy方向の両方をマイナス倍すると、原点(0,0)を境にして、上下左右が反転します。
このマイナス倍の関係性は自分で数値を変えてみて実験しておいてください。

次は回転行列にトライしてみましょう。

Matrix3x3で点を行列で回転(rotate:ローテーション)させる

main.cppを変更して、3点p0{1,1} 点p1{3,4} 点p2{5,2} を 回転行列で原点(0,0)を中心に反時計回りに60度(θ=60°)回転してしてみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "Matrix3x3.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p0{ 1,1 }; // 点p0
        Vector2 p1{ 3,4 }; // 点p1
        Vector2 p2{ 5,2 }; // 点p2

        constexpr float pi = 3.14159265359f;
        float rad = 60 * (pi / 180.0f);
        Matrix3x3 rotate{ std::cosf(rad),std::sinf(rad), 0,
                         -std::sinf(rad),std::cosf(rad), 0,
                                       0,             0, 1 }; // 回転行列
        Matrix3x3 scale = Matrix3x3::scale(Vector2{ -2,5 }); // スケール(拡大縮小)行列

        // 点q0,q1,q2
        Vector2 q0 = p0 * rotate; // 点p0×rotate (回転行列を右から掛け算)すると原点を中心に回転する
        Vector2 q1 = p1 * rotate; // 点p1×rotate (回転行列を右から掛け算)すると原点を中心に回転する
        Vector2 q2 = p2 * rotate; // 点p2×rotate (回転行列を右から掛け算)すると原点を中心に回転する

        // 三角形p0,p1,p2を描く
        mathGraph.DrawLine(p0.x, p0.y, p1.x, p1.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(p1.x, p1.y, p2.x, p2.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(p2.x, p2.y, p0.x, p0.y, GetColor(255, 255, 255));

        // 回転後の三角形q0,q1,q2を描く
        mathGraph.DrawLine(q0.x, q0.y, q1.x, q1.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(q1.x, q1.y, q2.x, q2.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(q2.x, q2.y, q0.x, q0.y, GetColor(255, 255, 255));

        // 回転前の3点を描く

        // 点p0を描く
        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        // 点p1を描く
        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        // 点p2を描く
        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        // 回転したあとの3点を描く

        // 点q0を描く
        mathGraph.DrawPoint(q0.x, q0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string q0_String = "q0=(" + std::to_string(q0.x) + "," + std::to_string(q0.y) + ")";
        mathGraph.DrawString(q0.x, q0.y, q0_String.c_str(), GetColor(255, 0, 0));

        // 点q1を描く
        mathGraph.DrawPoint(q1.x, q1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string q1_String = "q1=(" + std::to_string(q1.x) + "," + std::to_string(q1.y) + ")";
        mathGraph.DrawString(q1.x, q1.y, q1_String.c_str(), GetColor(0, 255, 0));

        // 点q2を描く
        mathGraph.DrawPoint(q2.x, q2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string q2_String = "q2=(" + std::to_string(q2.x) + "," + std::to_string(q2.y) + ")";
        mathGraph.DrawString(q2.x, q2.y, q2_String.c_str(), GetColor(0, 0, 255));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？原点(0,0)を中心として三角形が60度回転したでしょうか？
std::cosf関数やstd::sinf関数はラジアンで角度を入力する必要があるので、円周率piを使って60度を、float rad = 60 * (pi / 180.0f); のように単位:ラジアンに変換してます。

では、今回も今後を手軽にするために、Matrix3x3.hに回転行列を得る関数を追加して行列の数字を全部は手打ちせずに回転行列をゲットできるようにしておきましょう。

Matrix3x3.hを変更して回転行列をゲットするための関数を定義しましょう。

#ifndef MATRIX3X3_H_
#define MATRIX3X3_H_

#include "Vector2.h" // 2Dのベクトル

#include <ostream>
#include <cmath>

// 行列(3×3)　2Dにも3Dにも使う
struct Matrix3x3
{
    // 行列[行][列]の順 (行優先) https://qiita.com/suzuryo3893/items/9e543cdf8bc64dc7002a
    union
    {
        float m[3][3]{}; // 3×3の配列
        std::array<std::array<float, 3>, 3> mArr; // std::array型ベースなら少し便利
    };

    // float型のポインタへ(float*)キャストすればデータ配列 m の先頭のアドレスを返す
    inline operator float* () const { return (float*)m; }
    // float型のポインタへ(const float*)キャストすればデータ配列 m の先頭のアドレスを返す
    inline operator const float* () const { return (const float*)m; }

    // コンストラクタ
    Matrix3x3() = default;
    // コンストラクタ
    Matrix3x3(float m11, float m12, float m13,
        float m21, float m22, float m23,
        float m31, float m32, float m33)
        : m{ {m11, m12, m13}, {m21, m22, m23}, { m31, m32, m33} } {};

    // コンストラクタ (std::arrayで初期化版)
    Matrix3x3(std::array<std::array<float, 3>, 3>& matArr)
    {
        for (int j = 0; j < 3; ++j)
            for (int i = 0; i < 3; ++i)
                m[i][j] = matArr[i][j];
    }

    // ゼロ行列を返す
    static Matrix3x3 zero()
    {
        return Matrix3x3{ 0.0f, 0.0f, 0.0f,
                          0.0f, 0.0f, 0.0f,
                          0.0f, 0.0f, 0.0f };
    };

    // 単位行列を返す
    static Matrix3x3 identity()
    {
        return Matrix3x3{ 1.0f, 0.0f, 0.0f,
                          0.0f, 1.0f, 0.0f,
                          0.0f, 0.0f, 1.0f };
    };

    //[2D]拡大縮小行列を返す(2D向け)
    static Matrix3x3 scale(const Vector2& s)
    {
        return Matrix3x3{ s.x, 0.0f, 0.0f,
                          0.0f, s.y, 0.0f,
                          0.0f, 0.0f, 1.0f };
    };

    //[2D]回転行列を返す(2D向け) degree:角度(°) (DirectX系)
    static Matrix3x3 rotate(float degree)
    {
        constexpr float pi = 3.14159265359f;
        float rad = degree * (pi / 180.0f);
        float cos_theta = std::cos(rad), sin_theta = std::sin(rad);
        return Matrix3x3{ cos_theta, sin_theta, 0.0f,
                          -sin_theta, cos_theta, 0.0f,
                               0.0f,       0.0f, 1.0f };
    };

    //[2D]平行移動行列を返す(2D向け) (DirectX系)
    static Matrix3x3 translate(const Vector2& t)
    {
        return Matrix3x3{ 1.0, 0.0f, 0.0f,
                          0.0, 1.0f, 0.0f,
                          t.x, t.y, 1.0f };
    };

    // 転置行列を返す(メンバ関数版)
    inline Matrix3x3 transpose()
    {
        Matrix3x3 result;
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                result.m[i][j] = this->m[j][i]; // 行i と列j を行j と列i に交換

        return result;
    };

    /*-----　演算子オーバーロード　-----*/

    inline Matrix3x3 operator + () const { return *this; }

    // マイナスの符号を単体の行列につけたとき
    inline Matrix3x3 operator -() const
    {
        Matrix3x3 result;
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                result.m[i][j] = -this->m[i][j];
        return result;
    };

    inline Matrix3x3& operator += (const Matrix3x3& add)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] + add.m[i][j];
        return    *this;
    }

    inline Matrix3x3& operator -= (const Matrix3x3& sub)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] - sub.m[i][j];
        return    *this;
    }

    inline Matrix3x3& operator *= (const Matrix3x3& mul)
    {
        Matrix3x3 tmp; // 値を一時保管
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                tmp.m[i][j] = this->m[i][j];

        for (int i = 0; i < 3; ++i) {
            for (int j = 0; j < 3; ++j) {
                this->m[i][j] = 0;
                for (int k = 0; k < 3; ++k)
                    this->m[i][j] += tmp.m[i][k] * mul.m[k][j];
            }
        }
        return    *this;
    }

    inline Matrix3x3& operator *= (float multiply_num)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] * multiply_num;
        return    *this;
    }

    inline Matrix3x3& operator /= (float divide_num)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                this->m[i][j] = this->m[i][j] / divide_num;
        return    *this;
    }

    // 一致演算子行列の中身が全部一致するか一つでも違えばfalse
    inline bool operator == (const Matrix3x3& other)
    {
        for (int i = 0; i < 3; ++i)
            for (int j = 0; j < 3; ++j)
                if (this->m[i][j] != other.m[i][j]) return false;
        return    true;
    }

    // 不一致演算子
    inline bool operator != (const Matrix3x3& other)
    {
        return    !(*this == other);
    }

};

// 行列の加算
inline Matrix3x3 operator + (const Matrix3x3& left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left.m[i][j] + right.m[i][j];

    return result;
};

// 行列の減算
inline Matrix3x3 operator - (const Matrix3x3& left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left.m[i][j] - right.m[i][j];

    return result;
};

// 行列のスカラー倍 (スカラー×行列）
inline Matrix3x3 operator * (float left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left * right.m[i][j];

    return result;
};

// 行列のスカラー倍 (行列×スカラー）
inline Matrix3x3 operator * (const Matrix3x3& left, float right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = left.m[i][j] * right;

    return result;
};

// 行列の積
inline Matrix3x3 operator * (const Matrix3x3& left, const Matrix3x3& right)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i) {
        for (int j = 0; j < 3; ++j) {
            result.m[i][j] = 0;
            for (int k = 0; k < 3; ++k)
                result.m[i][j] += left.m[i][k] * right.m[k][j];
        }
    }
    return result;
};

//[2D]ベクトルと行列の積
inline Vector2 operator * (const Vector2& left, const Matrix3x3& right)
{
    float x = left.x * right.m[0][0] + left.y * right.m[1][0] + right.m[2][0];
    float y = left.x * right.m[0][1] + left.y * right.m[1][1] + right.m[2][1];
    return Vector2{ x, y };
};

inline const Matrix3x3 operator / (const Matrix3x3& left, const float right)
{
    return left * (1.0f / right);
}

// 転置行列を返す
inline Matrix3x3 transpose(const Matrix3x3& mat)
{
    Matrix3x3 result;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            result.m[i][j] = mat.m[j][i]; // 行i と列j を行j と列i に交換

    return result;
};

// 行列の出力
inline std::ostream& operator << (std::ostream& left, const Matrix3x3& right)
{
    for (int i = 0; i < 3; ++i) {
        for (int j = 0; j < 3; ++j) {
            left << right.m[i][j];
            if (j < 3 - 1) {
                left << " ";
            }
        }
        left << std::endl;
    }
    return left;
};

#endif

main.cppを変更して、3点p0{1,1} 点p1{3,4} 点p2{5,2} を 手軽にrotate関数でゲットした回転行列で原点(0,0)を中心に反時計回りに60度(θ=60°)回転してみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "Matrix3x3.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p0{ 1,1 }; // 点p0
        Vector2 p1{ 3,4 }; // 点p1
        Vector2 p2{ 5,2 }; // 点p2

        constexpr float pi = 3.14159265359f;
        float rad = 60 * (pi / 180.0f);
        Matrix3x3 rotate{ std::cosf(rad),std::sinf(rad), 0,
                         -std::sinf(rad),std::cosf(rad), 0,
                                       0,             0, 1 }; // 回転行列
        Matrix3x3 rotate = Matrix3x3::rotate(60); // 回転行列

        // 点q0,q1,q2
        Vector2 q0 = p0 * rotate; // 点p0×rotate (回転行列を右から掛け算)すると原点を中心に回転する
        Vector2 q1 = p1 * rotate; // 点p1×rotate (回転行列を右から掛け算)すると原点を中心に回転する
        Vector2 q2 = p2 * rotate; // 点p2×rotate (回転行列を右から掛け算)すると原点を中心に回転する

        // 三角形p0,p1,p2を描く
        mathGraph.DrawLine(p0.x, p0.y, p1.x, p1.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(p1.x, p1.y, p2.x, p2.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(p2.x, p2.y, p0.x, p0.y, GetColor(255, 255, 255));

        // 回転後の三角形q0,q1,q2を描く
        mathGraph.DrawLine(q0.x, q0.y, q1.x, q1.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(q1.x, q1.y, q2.x, q2.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(q2.x, q2.y, q0.x, q0.y, GetColor(255, 255, 255));

        // 回転前の3点を描く

        // 点p0を描く
        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        // 点p1を描く
        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        // 点p2を描く
        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        // 回転したあとの3点を描く

        // 点q0を描く
        mathGraph.DrawPoint(q0.x, q0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string q0_String = "q0=(" + std::to_string(q0.x) + "," + std::to_string(q0.y) + ")";
        mathGraph.DrawString(q0.x, q0.y, q0_String.c_str(), GetColor(255, 0, 0));

        // 点q1を描く
        mathGraph.DrawPoint(q1.x, q1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string q1_String = "q1=(" + std::to_string(q1.x) + "," + std::to_string(q1.y) + ")";
        mathGraph.DrawString(q1.x, q1.y, q1_String.c_str(), GetColor(0, 255, 0));

        // 点q2を描く
        mathGraph.DrawPoint(q2.x, q2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string q2_String = "q2=(" + std::to_string(q2.x) + "," + std::to_string(q2.y) + ")";
        mathGraph.DrawString(q2.x, q2.y, q2_String.c_str(), GetColor(0, 0, 255));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？原点(0,0)を中心として三角形が60度回転したでしょうか？
rotete関数の引数degreeの方は60度の角度のまま入力できるようにしてあるので、お手軽に好きな角度で回転行列をゲットできるようにしてあります。

Matrix3x3で点を組み合わせ行列(transform行列)で回転、スケール、平行移動させる

main.cppを変更して、3点p0{1,1} 点p1{3,4} 点p2{5,2} を transform行列でまずはscale行列だけを設定して、原点(0,0)を中心にスケーリングしてみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "Matrix3x3.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p0{ 0, 1 }; // 点p0
        Vector2 p1{-2,-1 }; // 点p1
        Vector2 p2{ 2,-1 }; // 点p2

        Matrix3x3 translate = Matrix3x3::translate(Vector2{ 2,3 }); // 平行移動行列
        Matrix3x3 scale = Matrix3x3::scale(Vector2{ 4,6 }); // スケール行列
        Matrix3x3 rotate = Matrix3x3::rotate(45); // 回転行列

        Matrix3x3 transform = scale; // 組み合わせ行列(スケール)

        // 点q0,q1,q2
        Vector2 q0 = p0 * transform; // 点p0×transform (組み合わせ行列を右から掛け算)するとスケールする
        Vector2 q1 = p1 * transform; // 点p1×transform (組み合わせ行列を右から掛け算)するとスケールする
        Vector2 q2 = p2 * transform; // 点p2×transform (組み合わせ行列を右から掛け算)するとスケールする

        // 三角形p0,p1,p2を描く
        mathGraph.DrawLine(p0.x, p0.y, p1.x, p1.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(p1.x, p1.y, p2.x, p2.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(p2.x, p2.y, p0.x, p0.y, GetColor(255, 255, 255));

        // 組み合わせ変換(transform)後の三角形q0,q1,q2を描く
        mathGraph.DrawLine(q0.x, q0.y, q1.x, q1.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(q1.x, q1.y, q2.x, q2.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(q2.x, q2.y, q0.x, q0.y, GetColor(255, 255, 255));

        // 組み合わせ変換(transform)前の3点を描く

        // 点p0を描く
        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        // 点p1を描く
        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        // 点p2を描く
        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        // 組み合わせ変換(transform)したあとの3点を描く

        // 点q0を描く
        mathGraph.DrawPoint(q0.x, q0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string q0_String = "q0=(" + std::to_string(q0.x) + "," + std::to_string(q0.y) + ")";
        mathGraph.DrawString(q0.x, q0.y, q0_String.c_str(), GetColor(255, 0, 0));

        // 点q1を描く
        mathGraph.DrawPoint(q1.x, q1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string q1_String = "q1=(" + std::to_string(q1.x) + "," + std::to_string(q1.y) + ")";
        mathGraph.DrawString(q1.x, q1.y, q1_String.c_str(), GetColor(0, 255, 0));

        // 点q2を描く
        mathGraph.DrawPoint(q2.x, q2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string q2_String = "q2=(" + std::to_string(q2.x) + "," + std::to_string(q2.y) + ")";
        mathGraph.DrawString(q2.x, q2.y, q2_String.c_str(), GetColor(0, 0, 255));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？まずは原点(0,0)を中心として三角形がスケール(拡大)したでしょうか？
つぎは、組み合わせ行列(transform行列)に回転行列を「右側から掛け算して、スケール→回転、の順に変換」してみましょう。

main.cppを変更して、3点p0{1,1} 点p1{3,4} 点p2{5,2} を transform行列に右側からrotate行列を掛け算して、原点(0,0)を中心にスケール→回転、の順に拡大回転してみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "Matrix3x3.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p0{ 0, 1 }; // 点p0
        Vector2 p1{-2,-1 }; // 点p1
        Vector2 p2{ 2,-1 }; // 点p2

        Matrix3x3 translate = Matrix3x3::translate(Vector2{ 2,3 }); // 平行移動行列
        Matrix3x3 scale = Matrix3x3::scale(Vector2{ 4,6 }); // スケール行列
        Matrix3x3 rotate = Matrix3x3::rotate(45); // 回転行列

        Matrix3x3 transform = scale * rotate; // 組み合わせ行列(スケール→回転)

        // 点q0,q1,q2
        Vector2 q0 = p0 * transform; // 点p0×transform (組み合わせ行列を右から掛け算)するとスケール→回転する
        Vector2 q1 = p1 * transform; // 点p1×transform (組み合わせ行列を右から掛け算)するとスケール→回転する
        Vector2 q2 = p2 * transform; // 点p2×transform (組み合わせ行列を右から掛け算)するとスケール→回転する

        // 三角形p0,p1,p2を描く
        mathGraph.DrawLine(p0.x, p0.y, p1.x, p1.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(p1.x, p1.y, p2.x, p2.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(p2.x, p2.y, p0.x, p0.y, GetColor(255, 255, 255));

        // 組み合わせ変換(transform)後の三角形q0,q1,q2を描く
        mathGraph.DrawLine(q0.x, q0.y, q1.x, q1.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(q1.x, q1.y, q2.x, q2.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(q2.x, q2.y, q0.x, q0.y, GetColor(255, 255, 255));

        // 組み合わせ変換(transform)前の3点を描く

        // 点p0を描く
        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        // 点p1を描く
        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        // 点p2を描く
        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        // 組み合わせ変換(transform)したあとの3点を描く

        // 点q0を描く
        mathGraph.DrawPoint(q0.x, q0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string q0_String = "q0=(" + std::to_string(q0.x) + "," + std::to_string(q0.y) + ")";
        mathGraph.DrawString(q0.x, q0.y, q0_String.c_str(), GetColor(255, 0, 0));

        // 点q1を描く
        mathGraph.DrawPoint(q1.x, q1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string q1_String = "q1=(" + std::to_string(q1.x) + "," + std::to_string(q1.y) + ")";
        mathGraph.DrawString(q1.x, q1.y, q1_String.c_str(), GetColor(0, 255, 0));

        // 点q2を描く
        mathGraph.DrawPoint(q2.x, q2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string q2_String = "q2=(" + std::to_string(q2.x) + "," + std::to_string(q2.y) + ")";
        mathGraph.DrawString(q2.x, q2.y, q2_String.c_str(), GetColor(0, 0, 255));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？三角形が、拡大してから→45度回転したでしょうか？
このようにtransform行列に順番にスケールや回転行列を掛け合わせることが、様々な位置や角度や大きさなどの姿勢をゲーム内に表示されるオブジェクトに適用している計算の正体なのです。
Unityで普段、gameobjectのtransformにx,y,zの位置や角度を設定していると思いますが、このtransfromの正体こそが組み合わせ行列にあたるとイメージにとどめておきましょう。
(厳密にいうと3Dの角度については回転行列ではなく、その上位互換の「クオータニオン」を使っています。)

では、実験のために今度は掛け算の順番をひっくり返し、rotate * scaleの順にして rotateで回転してから→scaleで回転、するとどうなるかやってみましょう。

main.cppを変更して、3点p0{1,1} 点p1{3,4} 点p2{5,2} を transform行列に右側からrotate行列を掛け算して、原点(0,0)を中心にスケール→回転、の順に拡大回転してみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "Matrix3x3.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p0{ 0, 1 }; // 点p0
        Vector2 p1{-2,-1 }; // 点p1
        Vector2 p2{ 2,-1 }; // 点p2

        Matrix3x3 translate = Matrix3x3::translate(Vector2{ 2,3 }); // 平行移動行列
        Matrix3x3 scale = Matrix3x3::scale(Vector2{ 4,6 }); // スケール行列
        Matrix3x3 rotate = Matrix3x3::rotate(45); // 回転行列

        Matrix3x3 transform = rotate * scale; // 組み合わせ行列(回転→スケール)

        // 点q0,q1,q2
        Vector2 q0 = p0 * transform; // 点p0×transform (組み合わせ行列を右から掛け算)すると回転→スケールする
        Vector2 q1 = p1 * transform; // 点p1×transform (組み合わせ行列を右から掛け算)すると回転→スケールする
        Vector2 q2 = p2 * transform; // 点p2×transform (組み合わせ行列を右から掛け算)すると回転→スケールする

        // 三角形p0,p1,p2を描く
        mathGraph.DrawLine(p0.x, p0.y, p1.x, p1.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(p1.x, p1.y, p2.x, p2.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(p2.x, p2.y, p0.x, p0.y, GetColor(255, 255, 255));

        // 組み合わせ変換(transform)後の三角形q0,q1,q2を描く
        mathGraph.DrawLine(q0.x, q0.y, q1.x, q1.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(q1.x, q1.y, q2.x, q2.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(q2.x, q2.y, q0.x, q0.y, GetColor(255, 255, 255));

        // 組み合わせ変換(transform)前の3点を描く

        // 点p0を描く
        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        // 点p1を描く
        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        // 点p2を描く
        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        // 組み合わせ変換(transform)したあとの3点を描く

        // 点q0を描く
        mathGraph.DrawPoint(q0.x, q0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string q0_String = "q0=(" + std::to_string(q0.x) + "," + std::to_string(q0.y) + ")";
        mathGraph.DrawString(q0.x, q0.y, q0_String.c_str(), GetColor(255, 0, 0));

        // 点q1を描く
        mathGraph.DrawPoint(q1.x, q1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string q1_String = "q1=(" + std::to_string(q1.x) + "," + std::to_string(q1.y) + ")";
        mathGraph.DrawString(q1.x, q1.y, q1_String.c_str(), GetColor(0, 255, 0));

        // 点q2を描く
        mathGraph.DrawPoint(q2.x, q2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string q2_String = "q2=(" + std::to_string(q2.x) + "," + std::to_string(q2.y) + ")";
        mathGraph.DrawString(q2.x, q2.y, q2_String.c_str(), GetColor(0, 0, 255));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかかでしょう？行列の掛け算の順番を変えると、組み合わせ行列でtransformした結果が変わりました。
このように、行列の掛け算する順番で結果が変わるので、掛け算する順番の意味をプログラミングする人はわかっていないと思った通りの動かし方を実現できません。

Unityなどでは、スケール→回転→平行移動の順に行列が掛け算されています。
掛け算で書くならscale * rotate * translate;の順番ですね。

では、次はこの順番で掛け算をしてみましょう。

main.cppを変更して、transform行列に右側から順にscale、rotate、translate行列を掛け算して、原点(0,0)を中心にスケール→回転→平行移動、の順に行列変換してみましょう。

#include "DxLib.h"

#include "Screen.h"
#include "Vector2.h"
#include "Matrix3x3.h"
#include "MathGraph2D.h"
#include "MyMath.h"

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
    // 画面モードの設定
    SetWindowSize(Screen::Width, Screen::Height);// ウィンドウサイズ960×540(こことSetGraphModeのサイズが異なると画像がゆがむ)
    SetGraphMode(Screen::Width, Screen::Height, 32); // 画面サイズ960×540のカラービット数32ビットで起動
    SetMainWindowText("数学のベクトルの練習");//この行でエラーになったら【設定】マルチバイト文字セットが間違ってるかも
    ChangeWindowMode(TRUE);//フルスクリーン表示かウィンドウ表示か
    SetAlwaysRunFlag(TRUE); // ウィンドウが非アクティブでも動作させる

    // ＤＸライブラリの初期化
    if (DxLib_Init() < 0)
    {
        // エラーが発生したら直ちに終了
        return -1;
    }

    SetMouseDispFlag(TRUE);// ここをFALSEにするとマウスカーソル非表示
    //表示しているスクリーンの後ろで隠れて次に描く画像を先に描くモード
    // これとペアでScreenFlip();でつぎのページと入れ替えでちらつきを防ぐ
    SetDrawScreen(DX_SCREEN_BACK);
    SetUseTransColor(FALSE); // 画像の指定色を透過する機能を無効化

    ScreenFlip();

    // 数学っぽくわかりやすくマス目を描いて、原点を画面の中心にして、10倍のスケールでみやすく描く
    MathGraph2D mathGraph{ {Screen::Width / 2 ,Screen::Height / 2 },10.0f,{1.0f,1.0f} };

    // アニメーション(パラパラ漫画)するにはWhile文
    while (ProcessMessage() == 0)
    {// ProcessMessage() == 0になるのは×ボタン押したときなど
        ClearDrawScreen(); // 画面をまっさらにリセット

        mathGraph.DrawGrid(GetColor(100, 100, 100)); // 100,100,100のグレーのグリッドでマス目を描く

        Vector2 p0{ 0, 1 }; // 点p0
        Vector2 p1{-2,-1 }; // 点p1
        Vector2 p2{ 2,-1 }; // 点p2

        Matrix3x3 translate = Matrix3x3::translate(Vector2{ 2,3 }); // 平行移動行列
        Matrix3x3 scale = Matrix3x3::scale(Vector2{ 4,6 }); // スケール行列
        Matrix3x3 rotate = Matrix3x3::rotate(45); // 回転行列

        Matrix3x3 transform = scale * rotate * translate; // 組み合わせ行列(スケール→回転→平行移動)

        // 点q0,q1,q2
        Vector2 q0 = p0 * transform; // 点p0×transform (組み合わせ行列を右から掛け算)するとスケール→回転→平行移動する
        Vector2 q1 = p1 * transform; // 点p1×transform (組み合わせ行列を右から掛け算)するとスケール→回転→平行移動する
        Vector2 q2 = p2 * transform; // 点p2×transform (組み合わせ行列を右から掛け算)するとスケール→回転→平行移動する

        // 三角形p0,p1,p2を描く
        mathGraph.DrawLine(p0.x, p0.y, p1.x, p1.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(p1.x, p1.y, p2.x, p2.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(p2.x, p2.y, p0.x, p0.y, GetColor(255, 255, 255));

        // 組み合わせ変換(transform)後の三角形q0,q1,q2を描く
        mathGraph.DrawLine(q0.x, q0.y, q1.x, q1.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(q1.x, q1.y, q2.x, q2.y, GetColor(255, 255, 255));
        mathGraph.DrawLine(q2.x, q2.y, q0.x, q0.y, GetColor(255, 255, 255));

        // 組み合わせ変換(transform)前の3点を描く

        // 点p0を描く
        mathGraph.DrawPoint(p0.x, p0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string p0_String = "p0=(" + std::to_string((int)p0.x) + "," + std::to_string((int)p0.y) + ")";
        mathGraph.DrawString(p0.x, p0.y, p0_String.c_str(), GetColor(255, 0, 0));

        // 点p1を描く
        mathGraph.DrawPoint(p1.x, p1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string p1_String = "p1=(" + std::to_string((int)p1.x) + "," + std::to_string((int)p1.y) + ")";
        mathGraph.DrawString(p1.x, p1.y, p1_String.c_str(), GetColor(0, 255, 0));

        // 点p2を描く
        mathGraph.DrawPoint(p2.x, p2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string p2_String = "p2=(" + std::to_string((int)p2.x) + "," + std::to_string((int)p2.y) + ")";
        mathGraph.DrawString(p2.x, p2.y, p2_String.c_str(), GetColor(0, 0, 255));

        // 組み合わせ変換(transform)したあとの3点を描く

        // 点q0を描く
        mathGraph.DrawPoint(q0.x, q0.y, 3, GetColor(255, 0, 0), TRUE);
        std::string q0_String = "q0=(" + std::to_string(q0.x) + "," + std::to_string(q0.y) + ")";
        mathGraph.DrawString(q0.x, q0.y, q0_String.c_str(), GetColor(255, 0, 0));

        // 点q1を描く
        mathGraph.DrawPoint(q1.x, q1.y, 3, GetColor(0, 255, 0), TRUE);
        std::string q1_String = "q1=(" + std::to_string(q1.x) + "," + std::to_string(q1.y) + ")";
        mathGraph.DrawString(q1.x, q1.y, q1_String.c_str(), GetColor(0, 255, 0));

        // 点q2を描く
        mathGraph.DrawPoint(q2.x, q2.y, 3, GetColor(0, 0, 255), TRUE);
        std::string q2_String = "q2=(" + std::to_string(q2.x) + "," + std::to_string(q2.y) + ")";
        mathGraph.DrawString(q2.x, q2.y, q2_String.c_str(), GetColor(0, 0, 255));

        ScreenFlip(); // 裏で描いておいたスクリーンを表画面にフリップ入れ替え
    }

    // キー入力待ちをする
    WaitKey();

    // ＤＸライブラリの後始末
    DxLib_End();

    // ソフトの終了
    return 0;
}

いかがでしょう？これでゲームで一般的な「スケール→回転→平行移動」のtransform変換でゲーム内のオブジェクトの姿勢が制御できるようになりました。
こういった行列の組み合わせの計算でゲーム内のキャラクターなどの位置や回転や平行移動の情報データが取り扱われているという確かなイメージを頭の中に持っておくことが大切です。
くれぐれも、ゲームのエンジンの手軽さに慣れて「ゲームとそれを支える数字の世界のつながりが、ミッシングリンクにならないように..」
行列やベクトルなどを意識せずとも、Unityは使いこなせますが、
少し踏み込んだプログラミングをしているサイトの記事に出会ったときに、行列やベクトルの知識不足が足かせとなる日が必ず来るはずです。
普段使いする、transformだからこそ、石橋をたたくように、その基礎知識こそ「あたりまえとして」強化しておく必要があります。

Vector2を使って簡単な直線などを描いてみる

operator +などを定義して、Vector2どうしの足し算などができるようにする

Unityの定義に習って、zeroベクトルupベクトルなどの定義を追加する

数学グラフクラスを作成して数学っぽいマス目を引いたり、画面上y方向プラス、画面中心(0,0)、(x,y)が(3,9)のとき(30,90)など 拡大した位置に描く

数学クラスMyMathを作成して円と円の当たり判定をしてみる

Vector2にベクトルの大きさを三平方の定理で計算するmagnitude関数を追加する

Vector2に内積dotと外積cross関数を追加してMyMathクラスで円と線の当たり判定をできるようにする

MyMathクラスで円と線が当たったら線に沿って押し戻す処理ができるようにする

MyMathクラスで線に垂直に下した点の影(射影)位置と線と点の最短距離を求める

MyMathクラスで線と線が交差するか判定する

MyMathクラスでレイ(光線)と線分(壁や床など)が交差するか判定する

MyMathクラスでレイ(光線)と線分(壁や床など)の交点を求める

MyMathクラスで線と線の交点を求める

MyMathクラスで壁(線)に対する点の反射(線の終点の反射位置と交点)を求める

MyMathクラスで壁(線)に対する円(半径r)の反射(円の中心点の反射位置と円の反射する瞬間の中心点)を求める

MyMathクラスでレイ光線と円(半径r)の当たり判定と交点を求める

Matrix3x3で点を行列で平行移動(translate)させる

Matrix3x3で点を行列でスケール(拡大縮小)させる

Matrix3x3で点を行列で回転(rotate:ローテーション)させる

Matrix3x3で点を組み合わせ行列(transform行列)で回転、スケール、平行移動させる

数学グラフクラスを作成して数学っぽいマス目を引いたり、画面上y方向プラス、画面中心(0,0)、(x,y)が(3,9)のとき(30,90)など拡大した位置に描く